Werbung
Diese Übung behandelt folgende Punkte:
- Wie stellt man eine Bedingung für eine maximal zulässige Last auf?
- Wie berechnet man den zulässigen Winkel eines abgespannten Seils?
- Wie vereinfacht man die Berechnung von symmetrischen Anordnungen?
Aufgabe
Eine Last von 10 kN soll mit einem Seil an zwei Aufhängepunkten befestigt werden. Die maximal zulässige Zugkraft des Seils beträgt 20 kN. Wie groß muss der Winkel Alpha sein, damit das Seil nicht reißt?

Lösung
Aufgrund der symmetrischen Aufhängung genügt die Betrachtung einer Seite.
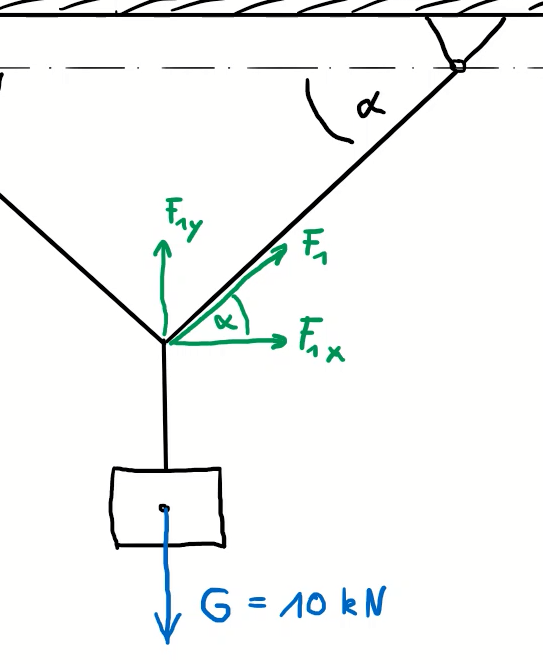
Die Vertikalkomponente der Seilkraft entspricht der halben Last G:
\[\tag{1} {F_{\mathit{1y}}}=\frac{G}{2}\]
und zur Seilkraft besteht die Beziehung
\[\tag{2} {F_1} \sin{\left( \alpha \right) }={F_{\mathit{1y}}}\]
\[\tag{3} F_1 = \frac{F_{1y}}{\sin\left( \alpha \right) }\]
Die Seilkraft soll nicht größer als 20 kN werden, also gilt
\[\tag{4} 20 kN \geq \frac{F_{1y}}{\sin\left( \alpha \right) }\]
\[\tag{5} \alpha \geq \arcsin \left( \frac{5 kN}{20 kN } \right) \]
\[\tag{6} \alpha \geq 14.48° \]
Werbung




