Werbung
Diese Übung beschäftigt sich mit folgenden Fragen:
- Wie berechnet man die Komponente einer Kraft?
- Wie berechnet man eine resultierende Kraft?
Aufgabe
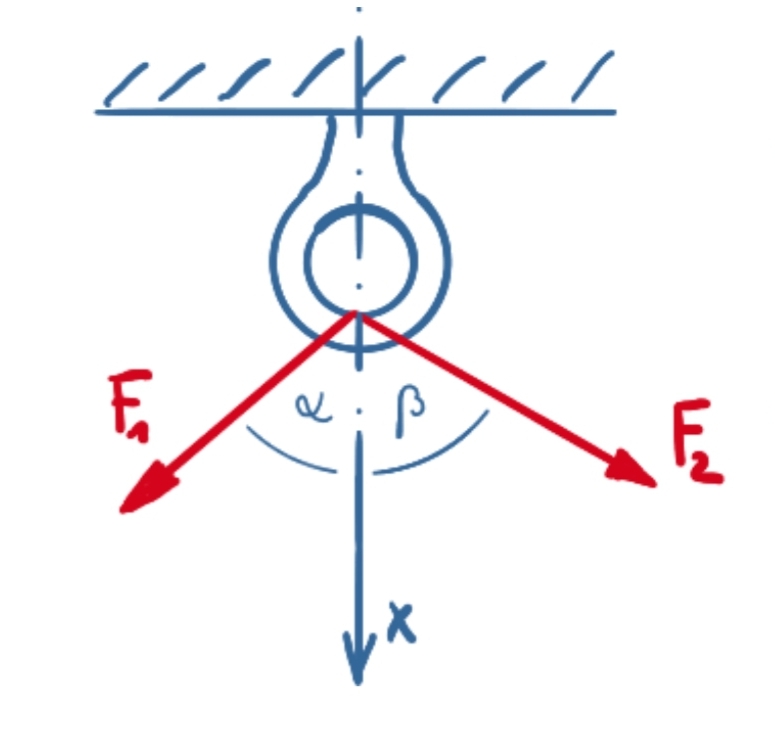
An einer Öse sind zwei Seile befestigt. Wie groß ist die Zugkraft an der Öse und wirkt diese in lotrechte Richtung?
geg.:F1 = 8,2 kN
F2 = 9,7 kN
α = 50°
β = 60°
Lösung
Die x-Komponenten der beiden angreifenden Kräfte ergeben
\[\tag{1} \sum F_x= F_1\cos(\alpha)+F_2\cos(\beta)\]
\[\tag{2} \sum F_x= 10.12 kN\]
Die Querrichtung der x-Achse als y-Achse angenommen, müsste eine lotrechte Kraft eine Querkomponente von Null haben. Dies wird geprüft durch
\[\tag{3} \sum F_y= -F_1\sin(\alpha)+F_2\sin(\beta)\]
\[\tag{4} \sum F_y= 2.12 kN\]
Die Querkraft ist nicht Null, die Zugkraft an der Öse wirkt also nicht lotrecht.
Die resultierende Kraft F setzt sich aus den x- und y-Komponenten wie folgt zusammen
\[\tag{5} F= \sqrt{F_x^2+F_y^2} \]
\[\tag{6} F = 10.34 kN\]
Kennen Sie schon die anderen Aufgaben zum Thema resultierende Kräfte berechnen?
Werbung




