This exercise is about the following questions:
- How to calculate a component of a force?
- How to calculate a resulting force?
Task
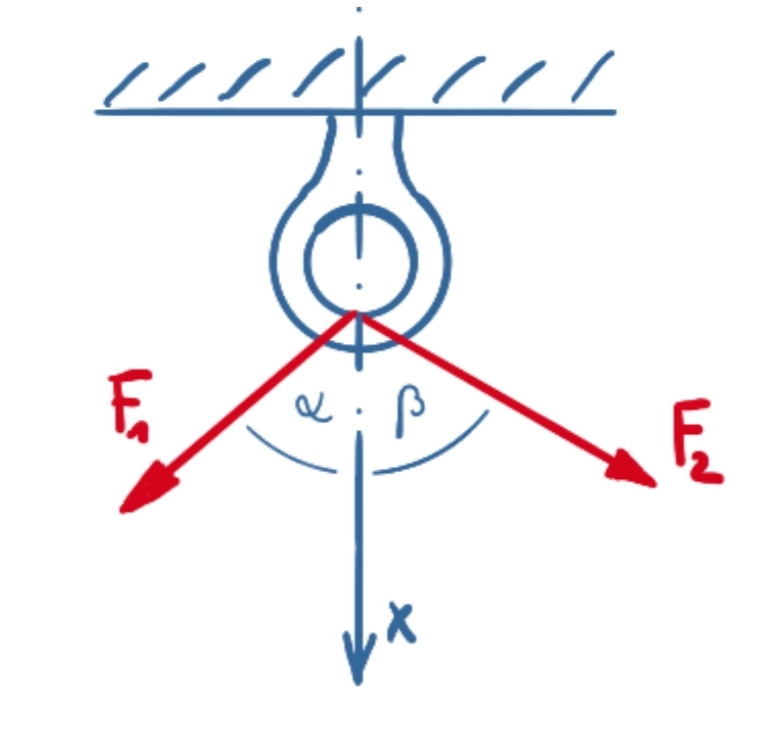
Two ropes are attached to an eyelet. Calculate the resulting tensile force on the eyelet. Does it act perpendicular?
given:F1 = 8,2 kN
F2 = 9,7 kN
α = 50°
β = 60°
Solution
The following video is in german language.
The x-components of the two forces result to
\[\tag{1} \sum F_x= F_1\cos(\alpha)+F_2\cos(\beta)\]
\[\tag{2} \sum F_x= 10.12 kN\]
Assuming the transverse direction of the x-axis as the y-axis, a perpendicularly force would have to have a transverse component of zero. This is checked by
\[\tag{3} \sum F_y= -F_1\sin(\alpha)+F_2\sin(\beta)\]
\[\tag{4} \sum F_y= 2.12 kN\]
The transverse force is not zero, so the tensile force on the eyelet does not act perpendicular.
The resulting force F ist calculated from the x- and y-components as follows:
\[\tag{5} F= \sqrt{F_x^2+F_y^2} \]
\[\tag{6} F = 10.34 kN\]
Do you already know the other exercises about resulting forces?

