This exercise is about how to determine a missing force and adresses the following questions:
- How to calculate a missing force by a given resultant force?
- How to determine the angle of a force?
- How to change equations and solve unknown values (or how to solve a simple equation system)?
Task
A ship is being pulled by three tugs. Tug 1 pulls with F1 = 7 kN, tug 2 with F2 = 6 kN. The force for tug 3 and its angle has to be calculated for a resultant force of 10 kN in x-direction.
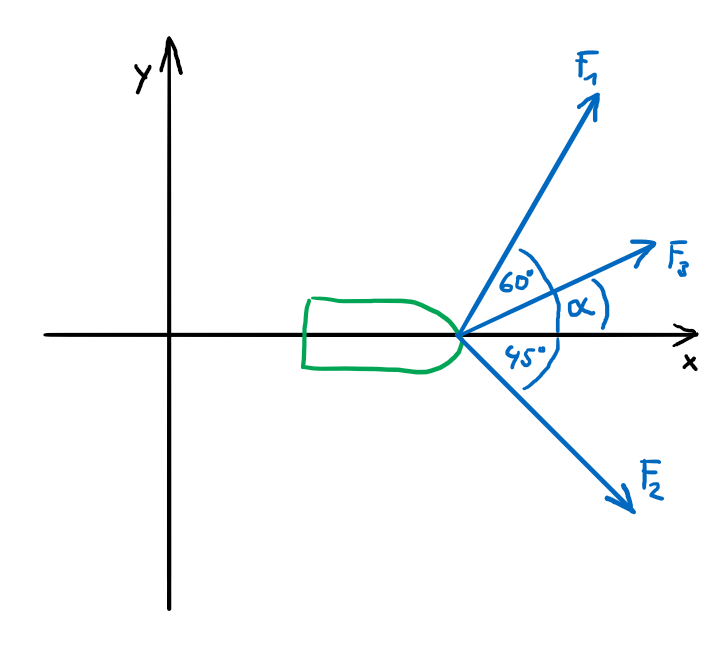
Solution
The following video is in german language.
The boundary conditions for the solution are: the sum of all forces in the x direction is 10 kN, the sum of all forces in the y direction is zero.
\[\tag{1} \sum F_x= 10 kN = F_1\cos(60°)+F_2\cos(45°)+F_3\cos(\alpha)\]
\[\tag{2} \sum F_y= 0 = F_1\sin(60°)-F_2\sin(45°)+F_3\sin(\alpha)\]
Equation 1 is solved for F3 and inserted into equation 2.
\[\tag{3} F_3= \frac{10 kN - F_1\cos(60°) - F_2\cos(45°)}{\cos(\alpha)}\]
\[\tag{4} 0 = F_1\sin(60°)-F_2\sin(45°)+\frac{10 kN - F_1\cos(60°) - F_2\cos(45°)}{\cos(\alpha)}\sin(\alpha) \]
Equation 4 is solved to
\[\tag{5} \alpha = \arctan\left(\frac{F_2\sin(45°)-F_1\sin(60°)}{10 kN - F_1\cos(60°) - F_2\cos(45°)}\right) \]
\[\tag{6} \alpha = -38.9° \]
and the missing force is
\[\tag{7} F_3 = 2.9 kN \]
Here we have some more exercises about resulting forces.

