This exercise shows how to calculate the permissible rope angle for a given load.
Task
A load of G = 10 kN has to be attached to two suspension points with ropes. The maximum permissible tensile force of the rope is 20 kN. What value must the angle α have so the rope doesn't break?

Solution
The following video is in german language.
Due to the symmetrical arrangement of the suspension, the look on one side is sufficient. It is a system of concurrent forces in a plane.
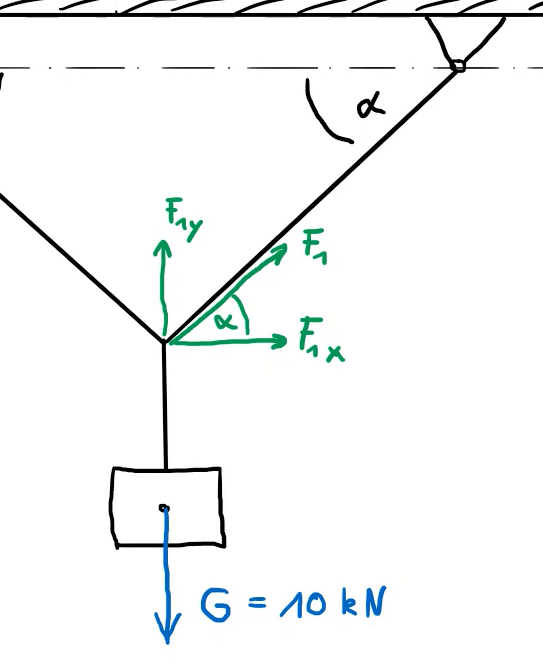
The vertical component of the rope force equals to the half of the load G:
\[\tag{1} {F_{\mathit{1y}}}=\frac{G}{2}\]
and the relationship to the rope force is
\[\tag{2} {F_1} \sin{\left( \alpha \right) }={F_{\mathit{1y}}}\]
\[\tag{3} F_1 = \frac{F_1y}{\sin\left( \alpha \right) }\]
The rope force shall not be greater than 20 kN, so the following applies
\[\tag{4} 20 kN \geq \frac{F_1y}{\sin\left( \alpha \right) }\]
\[\tag{5} \alpha \geq \arcsin \left( \frac{5 kN}{20 kN } \right) \]
\[\tag{6} \alpha \geq 14.48° \]
So the angle α must stay or be equal to 14.48°, or the rope will break. This was the way to calculate it for a symmetrical setup. We have another exercise, where an asymetrical layout is investigated, just take a look into the category Engineering Mechanics I in the menu at the side.
This was the exercise about how to calculate the permissible rope angle if you have a given load and maximum rope force. If you enjoyed it, please share it!

