This exercise investigates an asymmetrical load on two ropes and is about how to determine geometrical conditions for a force in a concurrent force system.
Task
A weight load of G = 100 N shall be suspended from two ropes 1 and 2 in such a way that the dimensions a = 2 m and h = 2 m are met and the force in rope 1 reach the value S1 = 80 N. How long must the distance between the two supports, hereby referred as l, be?
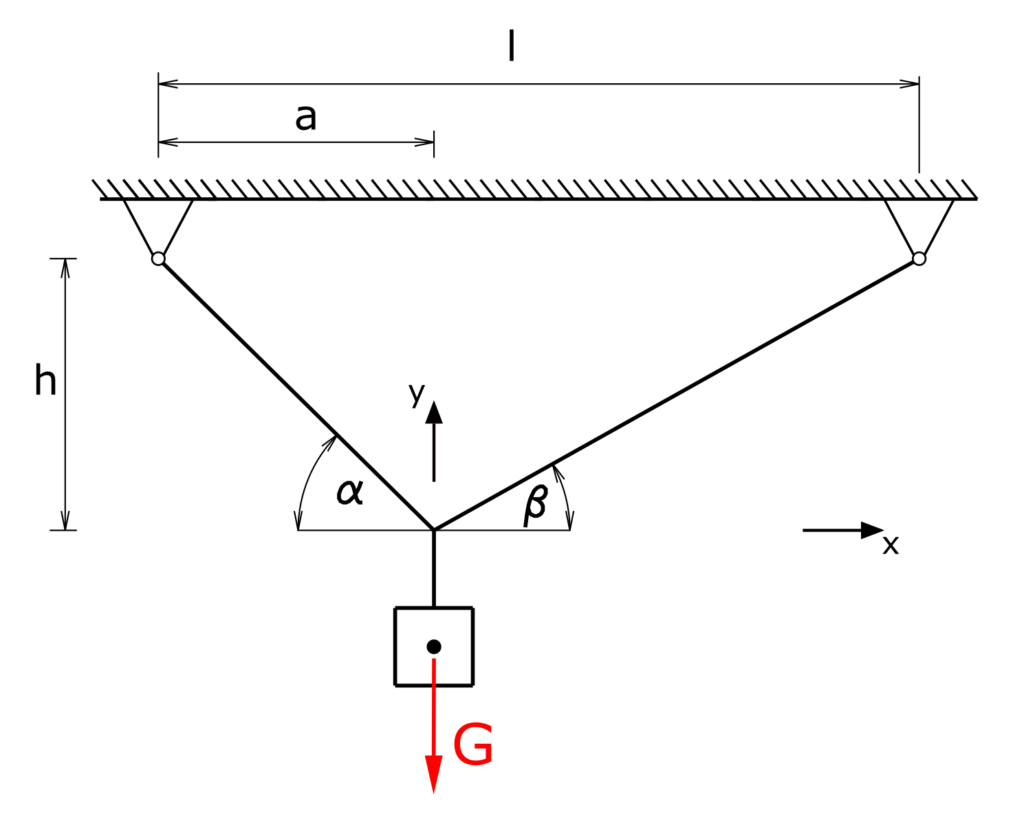
Solution
The following video is in german language. Please scroll down for the written solution.
The load G splits into the two rope forces S1 and S2.
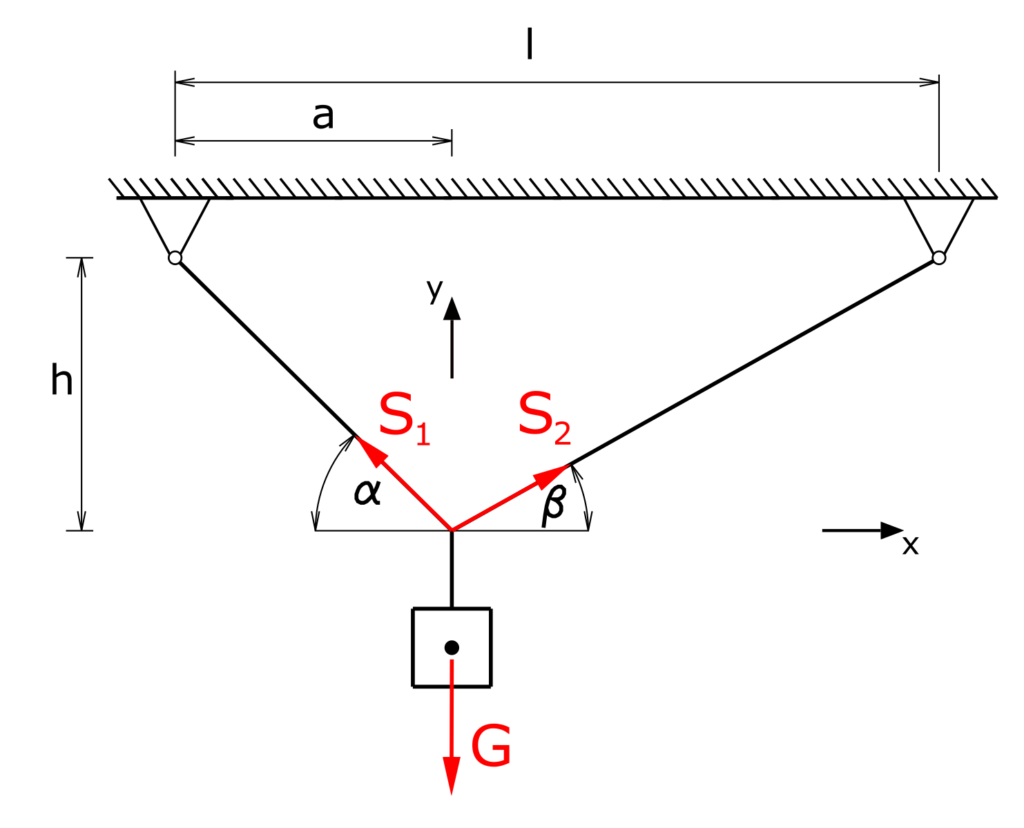
At the connection point of the ropes a concurrent force system establishes. All forces act at the same central point. (The forces S1 and S2 are drawn side by side for readability, both are acting on the same point.)
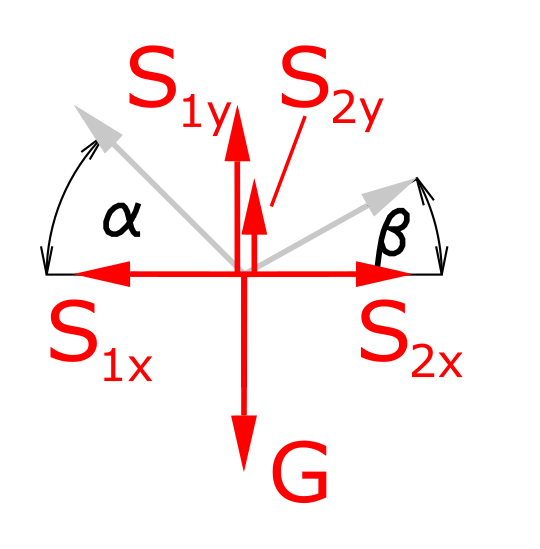
The equilibria of forces for the x and y directions are established. For this purpose, the rope forces are broken down into their respective components.
\[\tag{1} \sum F_x = 0 = -S_{1x} + S_{2x} \]
\[\tag{2} \sum F_y = 0 = S_{1y} + S_{2y} - G \]
The angle α can be calculated from the given lengths h and a.
\[\tag{3} \alpha = arctan \left( \frac{h}{a} \right) = 45° \]
With this angle and the specified force for rope 1, the x-components of the force in rope 1 can be calculated.
\[\tag{4} S_{1x} = S_1 cos \alpha \]
\[\tag{5} S_{1x} = 80 N \cdot cos 45° = 56.6 N \]
\[\tag{6} S_{2x} = S_{1x} = 56.6 N \]
And also the y component.
\[\tag{7} S_{1y} = S_1 sin \alpha \]
\[\tag{8} S_{1y} = 80 N \cdot sin 45° = 56.6 N \]
From equation 2 follows
\[\tag{9} S_{2y} = G - S_{1y} \]
\[\tag{10} S_{2y} = 100 N - 56.6 N = 43.4 N \]
The force in rope 2 is calculated using the Pythagorean theorem.
\[\tag{11} S_2 = \sqrt{S_{2x}^2 + S_{2y}^2} \]
\[\tag{12} S_2 = \sqrt{56.6^2 N^2 + 43.4^2 N^2} = 71.3 N \]
The angle β results from
\[\tag{13} S_{2x} = S_2 cos \beta \]
\[\tag{14} \beta = arccos \left( \frac{S_{2x}}{S_2} \right) = 37.5° \]
The angle β is related to h, l and a. The required length l can now be calculated from this.
\[\tag{15} \beta = arctan \left( \frac{h}{l-a} \right) \]
\[\tag{16} tan \beta = \frac{h}{l-a} \]
\[\tag{17} l = \frac{h}{tan \beta} + a = 4.6 m \]
So this was the way to determine geometrical conditions for an asymmetrical load on two ropes. Here we have a quite similar exercise about a symmetrical suspended load on two ropes.
Don't miss the other exercises regarding Engineering Mechanics 1!

