Werbung
Dieser Artikel führt verschiedene thermische Betrachtungen an einem Konstruktionsbeispiel ("Gerät") auf. Die hier gezeigten Schritte dienen der überschlägigen Auslegung in der Entwicklung und Konstruktion, wie sie z.B. zur Festlegung auf ein bestimmtes Kühlungskonzept von Geräten mit Wärmequellen genutzt werden können.
Die Ausgangssituation
Es soll ein Gerät entwickelt werden, in dem sich u.a. eine Wärmequelle (z.B. Leistungselektronik) befindet. Um eine sichere Bedienung zu gewährleisten, soll eine bestimmte Oberflächentemperatur des Gehäuses nicht überschritten werden. Die äußere Form des Geräts gleicht weitgehend einem Quader. Die Abmessungen stehen bereits fest und betragen:
Länge: 400 mm
Höhe: 400 mm
Breite: 500 mm
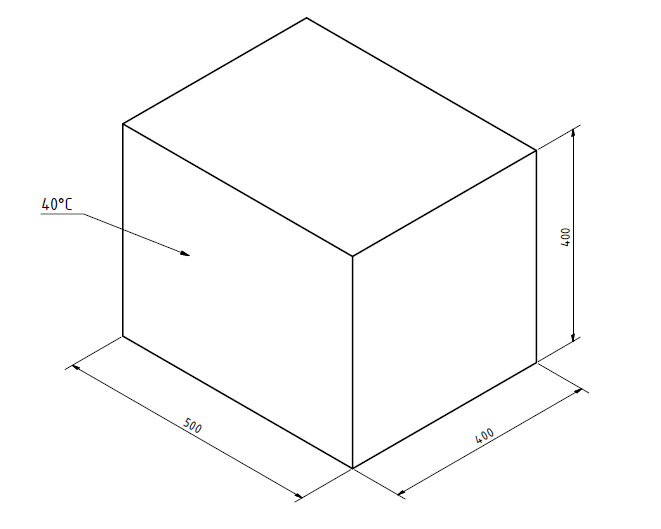
Das Gehäusematerial soll eine Aluminiumlegierung sein und eine Wandstärke von 5 mm haben. Die thermische Leistung der Wärmequelle beträgt 600 W. Die Wärmequelle ist mittig angeordnet und die Luft kann sich im Inneren des Geräts frei bewegen. Der Aufstellungsort des Gerätes ist windstill mit einer maximalen Umgebungstemperatur von 30°C. Es ist von allen Seiten weitestgehend zugänglich, d.h. es steht nicht auf einer Oberfläche.
Es stellen sich folgende Fragen:
A) Kann eine maximale Gehäusetemperatur von 40°C eingehalten werden?
B) Müssen konstruktive Maßnahmen zur Kühlung vorgesehen werden?
Lösungsansatz
In den nachfolgenden Berechnungen wird zur Vereinfachung nur mit der äußeren Fläche des Quaders gerechnet.
Überprüfung der Wärmeströme
Das Gerät wird sich im Betrieb so lange aufheizen, bis sich das Gleichgewicht zwischen der abgegebenen und zugeführten Wärmeleistung einstellt, d.h. es handelt sich dann um eine stationäre Wärmeübertragung.
Um die Berechnung zu vereinfachen, wird im ersten Schritt abgeschätzt, wie groß die durch Wärmestrahlung abgegebene Leistung ist. Da mit der maximal zulässigen Gehäusetemperatur ein konkreter Betriebspunkt gegeben ist, kann für diesen der Wärmestrom durch Strahlung berechnet werden.
Strahlung
Die Gleichung zur Berechnung der Strahlungswärme lautet
\[ P_S = \epsilon \cdot \sigma \cdot A \cdot T^4 \]
Benötigt werden also die Emissionszahlen für das Gehäusematerial bei der zu betrachtenden Temperatur. Bei kleineren Temperaturen können die Emissionszahlen als konstant angesehen werden, so dass für den hier vorliegenden Fall folgende Werte verwendet werden (für Aluminium eloxiert bei 70°C aus dieser Quelle).
\[ \epsilon_{min} = 0.67\]
\[ \epsilon_{max} = 0.95\]
Die Stefan-Boltzmann-Konstante ist
\[ \sigma = 5.670374419 \cdot 10^{-8} \frac{W}{m^2K^4} \]
Und die Oberfläche des Geräts beträgt
\[ A = 1.12m^2 \]
Damit liegt der Wärmestrom durch Strahlung durch die Bandbreite der Emissionszahl in einem Bereich von
\[ P_S = 409 ... 580W \]
D.h. die Wärmeabgabe allein durch Strahlung genügt nicht. Es muss betrachtet werden, ob die restliche Wärmeleistung durch freie Konvektion abgeführt werden kann.
Konvektion
Um die maximale Gehäusetemperatur einzuhalten, müsste die folgende Wärmeleistung durch Konvektion abgeführt werden.
\[ P_{Ksoll} = 600 W - 409 W = 191 W \]
Die Gleichung zur Berechnung des Wärmestroms durch Konvektion lautet
\[ P_{K} = \alpha \cdot A \cdot \Delta T \]
Der Wärmeübergangskoeffizient für Luft (bzw. allgemein für Gase) liegt bei freier Konvektion zwischen
\[ \alpha_{min} = 3 \frac{W}{m^2K}\]
\[ \alpha_{max} = 20 \frac{W}{m^2K} \]
Die Temperaturdifferenz zwischen Gehäusewand und Umgebungsluft beträgt
\[ \Delta T = 10 K \]
D.h. der tatsächlich durch Konvektion abgeführte Wärmestrom liegt im Bereich von
\[ P_{K} = 34 ... 224 W \]
Das bedeutet, dass die Oberflächentemperatur im ungünstigsten Fall über die gewünschten 40°C steigen wird.
Konstruktive Maßnahmen
Es sind verschiedene konstruktive Maßnahmen denkbar, um die Wärme abzuführen. Ein einfacher Lösungsansatz besteht darin, die Oberfläche zu vergrößern.
Um die notwendige Fläche zu bestimmen, werden nun die Gleichungen für den Wärmestrom durch Konvektion und den Wärmestrom durch Strahlung zusammengeführt zu einem Gesamtwärmestrom und die jeweils ungünstigsten Koeffizienten eingesetzt (Diese Gesamtrechnung könnte man auch gleich
zu Beginn durchführen, um die sich ergebende Temperaturdifferenz zu ermitteln). Als Wärmestrom wird die gegebene Leistung der Wärmequelle eingesetzt, die Gleichung kann dann nach der Soll-Fläche umgestellt werden.
\[ P_{ges} = α_{min} \cdot A_{soll} \cdot ΔT + A_{soll} \cdot T^4 \cdot ε_{min} \cdot σ \]
\[ A_{soll} = 1.52 m^2 \]
Wie lässt sich das konstruktiv umsetzen? Eine günstige Lösung wäre, die Seitenwände als Kühlrippen zu gestalten. Das bedeutet jedoch, dass zusätzlicher Bauraum benötigt wird.
Angenommen, eine Kühlrippe hat eine Tiefe von 10 mm und eine Breite von 2 mm. Damit beträgt die Fläche, die sie zusätzlich zur vorhandenen Geometrie beiträgt
\[ A_{K} = 8000mm^2 \]
Die notwendige Anzahl der Kühlrippen ergibt sich aus
\[ n_{K} = \frac{A_{soll}-A}{A_K} \approx 50 \]
Diese Kühlrippen können beliebig auf die Seitenwände des Gerätes verteilt werden. Kompakt auf einer Seite könnte es z.B. folgendermaßen aussehen:

Die Wärmeabfuhr nach außen wäre damit gelöst. Aber genügt das schon?
Überprüfung der Innentemperatur
Um eine Oberflächentemperatur von 40°C zu erreichen, muss die Wärme den Wärmewiderstand der Außenwand überwinden. Dazu muss die Innentemperatur höher sein als die Außentemperatur. Es handelt sich um einen Wärmedurchgang durch eine ebene Wand, der nach folgender Gleichung berechnet werden kann.
\[ P_{ges} = k \cdot A \cdot \left( T_i - T_a \right) \]
Ti ist die Innentemperatur, Ta die Außentemperatur. Der Term kA errechnet sich aus der Summe der Einzelwiderstände, hierbei ist wieder zu berücksichtigen, dass die Wärmeübergangskoeffizienten minimale und maximale Werte annehmen können.
\[ \frac{1}{k \cdot A} = \frac{1}{\alpha_i A} + \frac{\delta}{\lambda A} + \frac{1}{\alpha_a A} \]
Der Wärmeleitwert für Aluminium beträgt ca. 200 W/(mK), δ ist die Wandstärke der Gehäusewand mit 5 mm. Mit diesen Werten ergeben sich, insbesondere stark abhängig von den Wärmeübergangskoeffizienten, folgende mögliche Innentemperaturen
\[ T_i = 79°C ... 303°C \]
Ob diese Werte nun zulässig sind, hängt davon ab, was im Inneren des Gerätes passieren soll. Bei elektronischen Bauteilen sollten i.d.R. Werte von 65° C nicht überschritten werden, d.h. für diesen Fall müsste auf jeden Fall eine aktive Kühlung, also möglicherweise ein Gebläse eingesetzt werden. Bei Einsatz eines Gebläses könnte dann auch auf die vorab beschriebenen Kühlrippen verzichtet werden, insbesondere da sich durch die Luftbewegung an der Innenwand des Gehäuses ein günstigerer Wärmeübergangskoeffizient einstellt.
Bestimmung des erforderlichen Luftstroms
Es ist sinnvoll, für die Temperatur der Abluft auch einen Grenzwert festzulegen. In Annäherung an die maximal zulässige Oberflächentemperatur werden hier 50°C gewählt. D.h. die Temperaturspanne für den Abtransport der Wärme beträgt damit 20 K. Mit der spezifischen Wärmekapazität von cp = 1,001 kJ/(kgK) und einer Dichte von ρ = 1,293 kg/m3 für Luft (man könnte hier noch in Abhängigkeit von der Luftfeuchtigkeit genauere Betrachtungen durchführen) ergibt sich folgender Volumenstrom:
\[ P_{ges} = \dot{V} \cdot \rho \cdot c_p \cdot \Delta T \]
\[ \dot{V} = 0.023 \frac{m^3}{s} \]
Einen Gebläsedurchmesser von 150 mm angenommen, liegt die Strömungsgeschwindigkeit damit bei v = 1,3 m/s. Diese Werte liegen in einem angemessenen Rahmen, insbesondere da damit zu rechnen ist, dass nicht die gesamte Wärmeleistung über das Gebläse abgeführt werden muss.
Fazit
Damit ist die überschlägige Ermittlung der thermischen Bedingungen abgeschlossen. Die geforderten Temperaturen können eingehalten werden, wenn eine aktive Luftkühlung mit einem Gebläse eingesetzt wird.
Für genauere Betrachtungen sollte eine Simulationsrechnung hinzugezogen werden.
Werbung




