This exercise shows how to calculate the resulting moment from several forces acting under different angles in a plane state.
Task
There are three forces attacking on a cranked body. Which moment results from the forces F1, F2 and F3 regarding to point P?
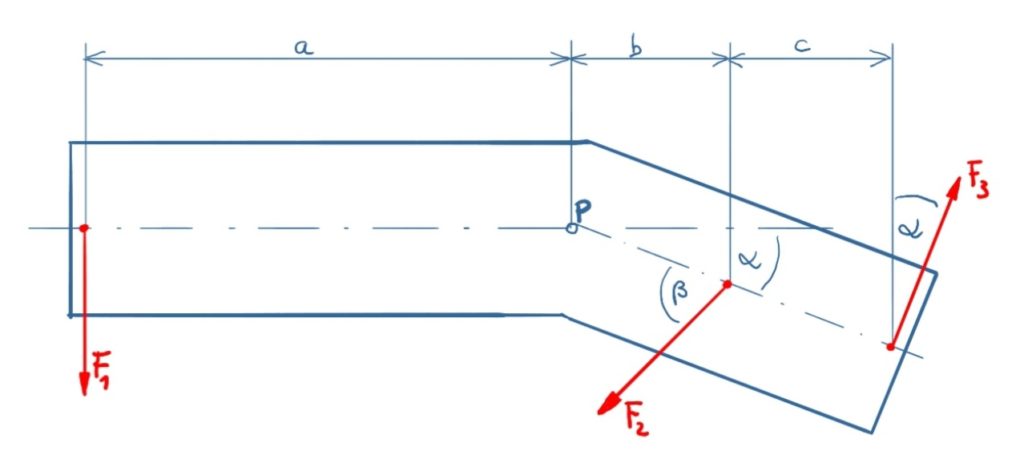
Solution
The following video is in german language. Please scroll down for the written solution.
Solution sketch
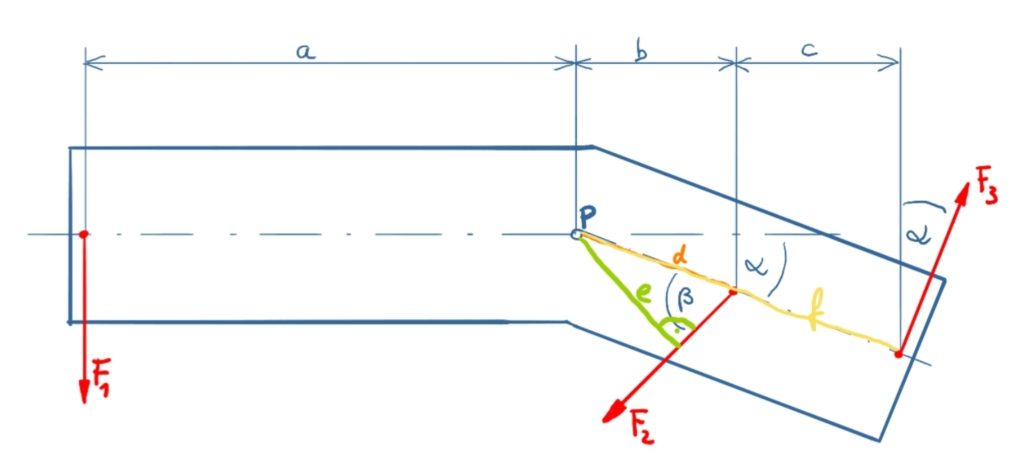
Approach
In the following solution, counterclockwise torques are defined as positive. In the solution sketch, the lever arms for the forces F2 are marked in green (distance e) and F3 light orange (distance f).
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]The resulting moment in point P is
\[\tag{1} M_P = F_1 \cdot a - F_2 \cdot e + F_3 \cdot f \]
The lever arm e results from:
\[\tag{2} e = d \cdot \sin \beta \]
The distance d results from
\[\tag{3} d = \frac{b}{\cos \alpha} \]
Inserted in equation 2 it gives
\[\tag{4} e = \frac{b}{\cos \alpha} \cdot \sin \beta \]
The segment f results from
\[\tag{5} f = \frac{b+c}{\cos \alpha} \]
The resulting moment at point P is finally
\[\tag{6} M_P = F_1 \cdot a - F_2 \cdot \frac{b}{\cos \alpha} \cdot \sin \beta + F_3 \cdot \frac{b+c}{\cos \alpha} \]
So this is the resulting moment from several forces regarding point P. Maybe you want to try for yourself to define another point, maybe the base of F1 and calculate the resulting moment for this case. Is it the same value?
There is another exercise for the three-dimensional calculation of resulting moments and forces where we show the calculation of the moments for two different points at a frame. You can find this exercise here.
Don't miss the other exercises regarding Engineering Mechanics 1!

