Werbung
Mit Klick auf das jeweilige Bild geht es zur Formel für den jeweiligen Flächenschwerpunkt:
Allgemeine Informationen und Übungen zur Berechnung von Flächenschwerpunkten gibt es unter dem Schlagwort Schwerpunkt.
Flächenschwerpunkte in der Ebene
Dreieck
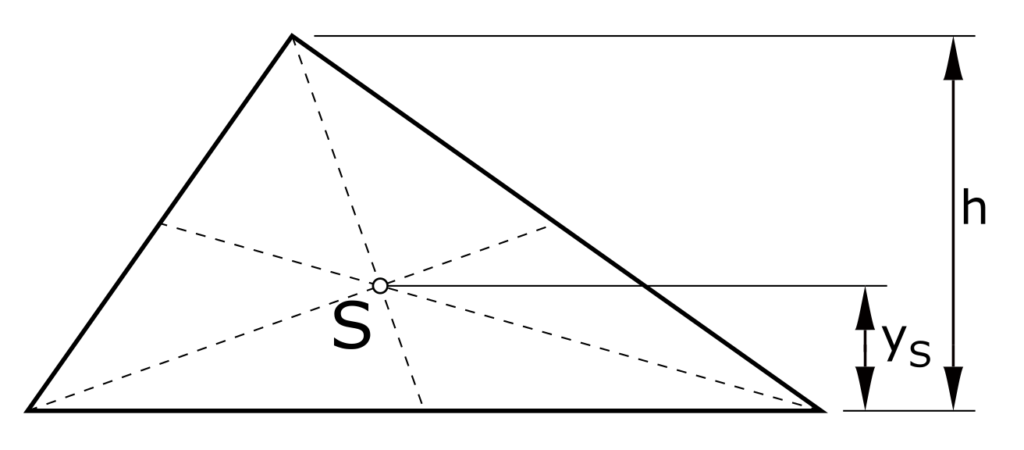
\[ y_S = \frac{h}{3}\]
Parallelogramm
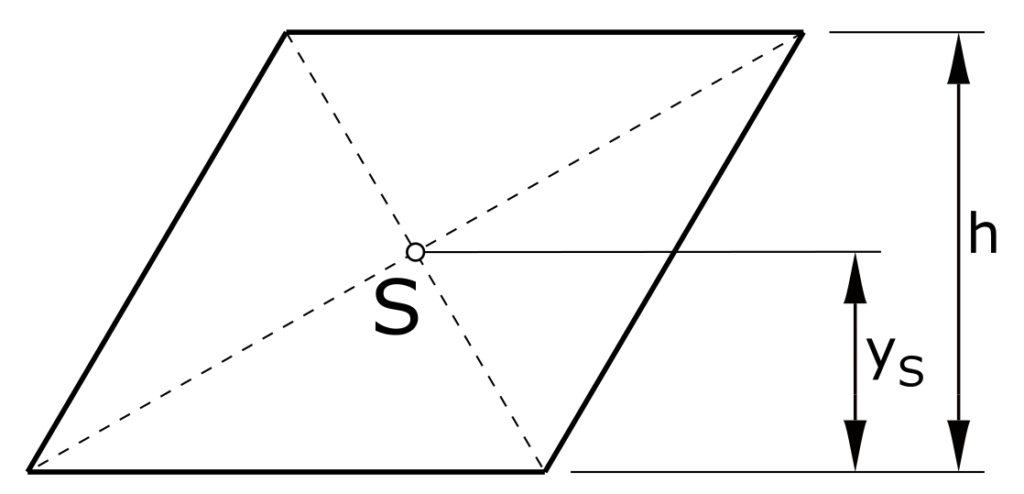
\[ y_S = \frac{h}{2}\]
Trapez
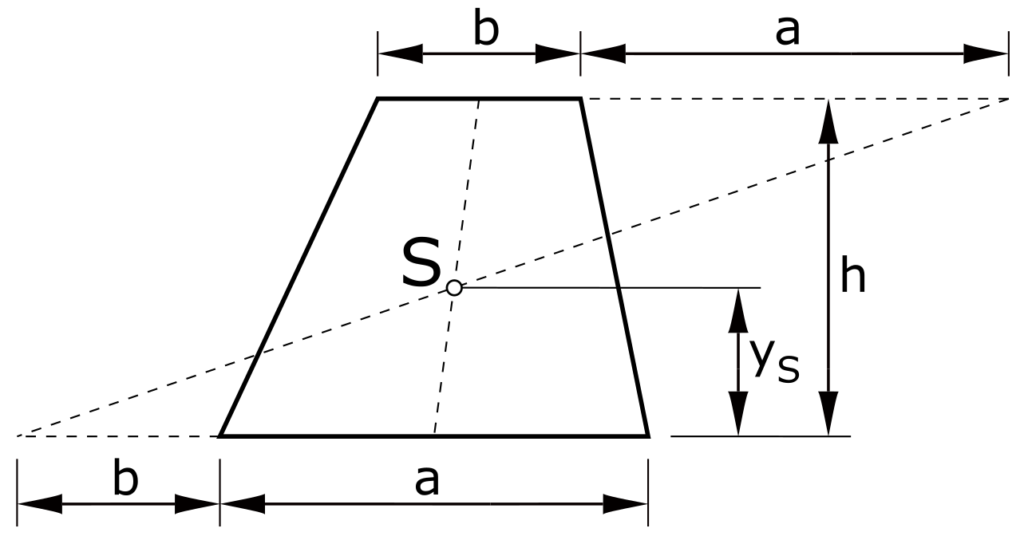
\[ y_S = \frac{h}{3} \cdot \frac{a+2\cdot b}{a+b}\]
Kreisausschnitt
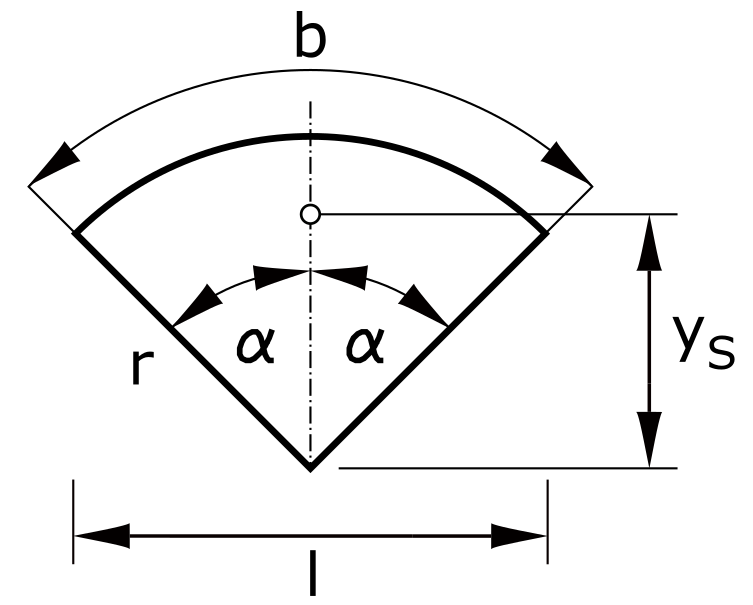
\[ y_S = \frac{2 \cdot r \cdot sin \alpha}{3 \cdot \alpha}\]
\[ y_S = \frac{2 \cdot r \cdot l}{3 \cdot b}\]
Für eine Halbkreisfläche gilt
\[ y_S = \frac{4 \cdot r }{3 \cdot \pi}\]
Kreisabschnitt
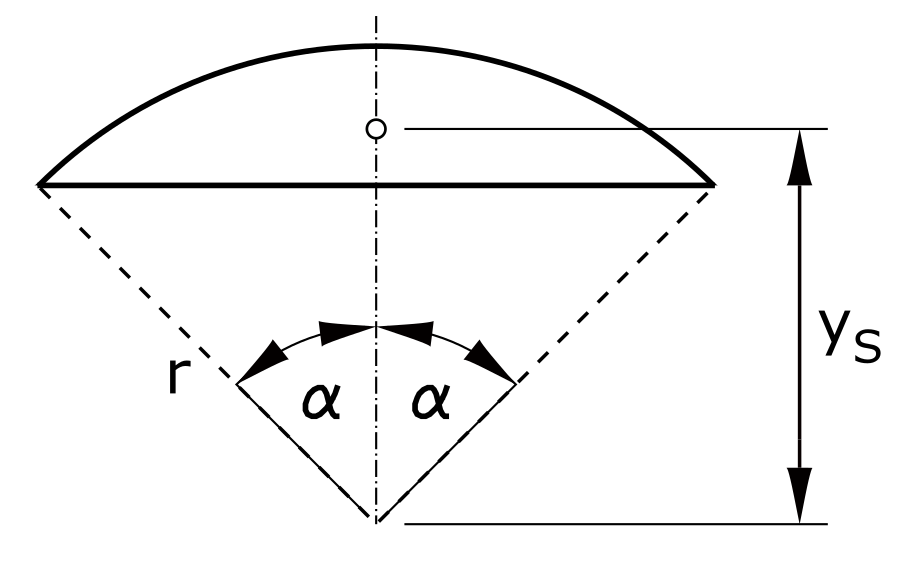
\[ y_S = \frac{2}{3} \cdot \frac{r \cdot sin^3 \alpha}{\alpha - sin \alpha \cdot cos \alpha} \]
Für eine Halbkreisfläche gilt
\[ y_S = \frac{4 \cdot r }{3 \cdot \pi}\]
Kreisringstück
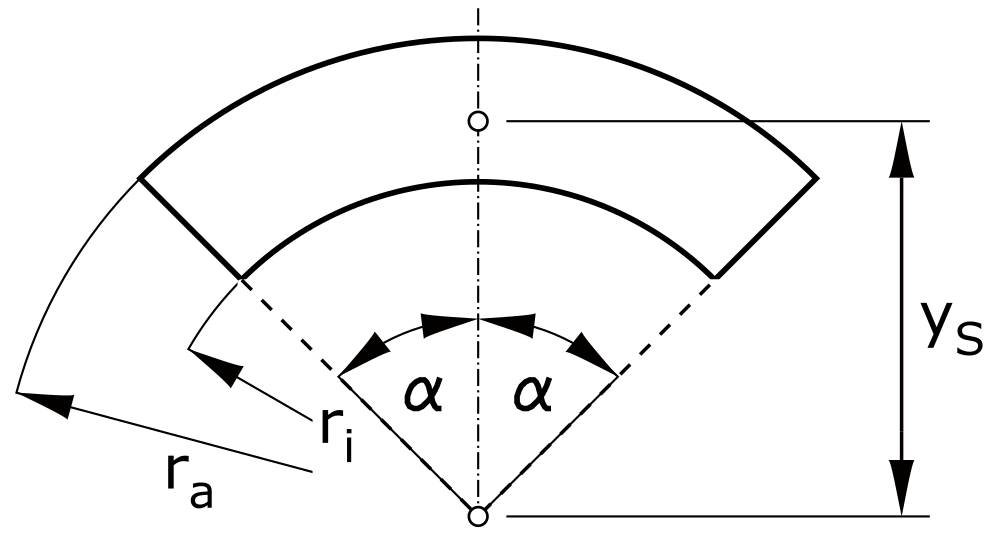
\[ y_S = \frac{2}{3} \cdot \frac{\left( r_a^3-r_i^3 \right) \cdot sin \alpha}{\left( r_a^2-r_i^2\right) \cdot \alpha} \]
Parabelflächen
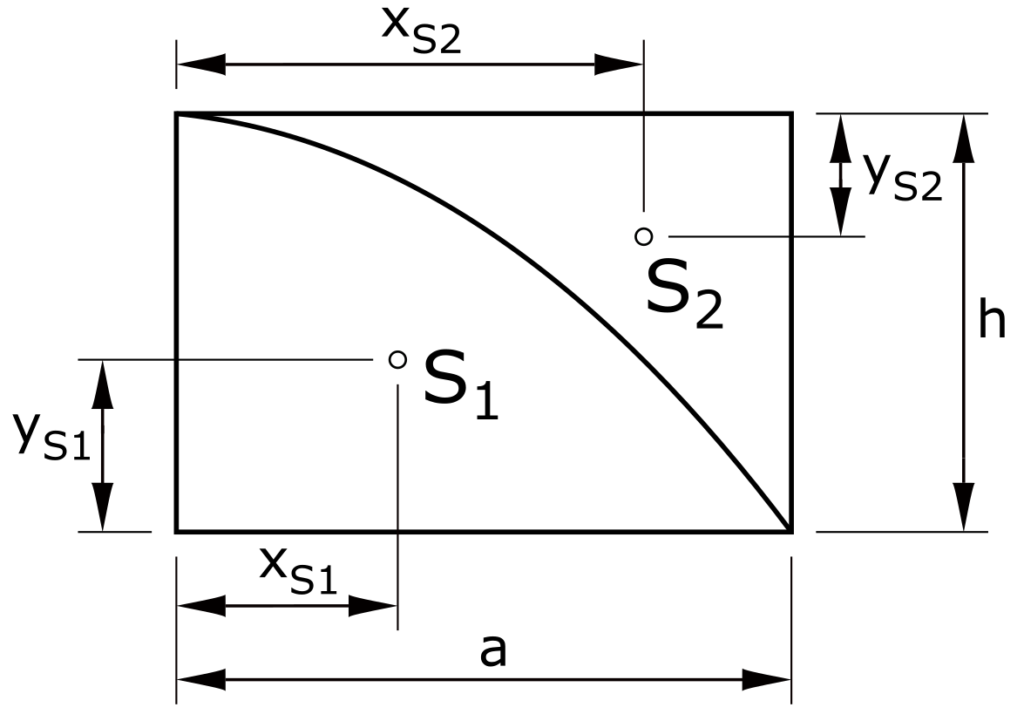
Schwerpunkt S1
\[ x_{S1} = \frac{3 \cdot a}{8} \]
\[ y_{S1} = \frac{2 \cdot h}{5} \]
Schwerpunkt S2
\[ x_{S2} = \frac{3 \cdot a}{4} \]
\[ y_{S2} = \frac{3 \cdot h}{10} \]
Parabelabschnitt
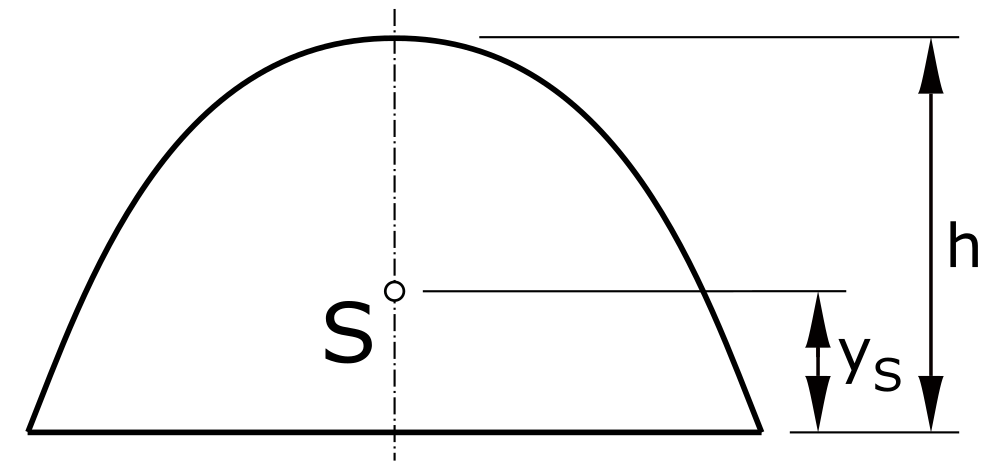
\[ y_S = \frac{2 \cdot h}{5} \]
Ellipsenabschnitt
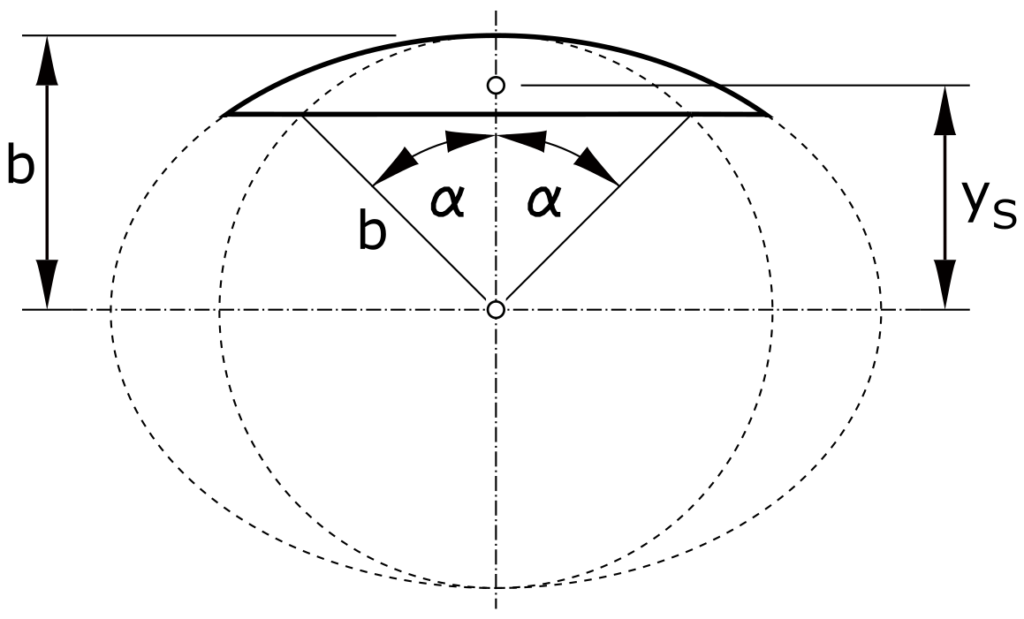
\[ y_S = \frac{2 }{3} \cdot \frac{b \cdot sin^3 \alpha}{\alpha - sin \alpha \cdot cos \alpha} \]
Wenn Sie mehr suchen als den Flächenschwerpunkt: hier geht es zur Berechnung von mechanischen Eigenschaften von Querschnitten.
Werbung




