Werbung
In dieser Übung werden die Lagerreaktionen für einen statisch überbestimmten Träger mit Hilfe der Biegelinie berechnet.
Aufgabe
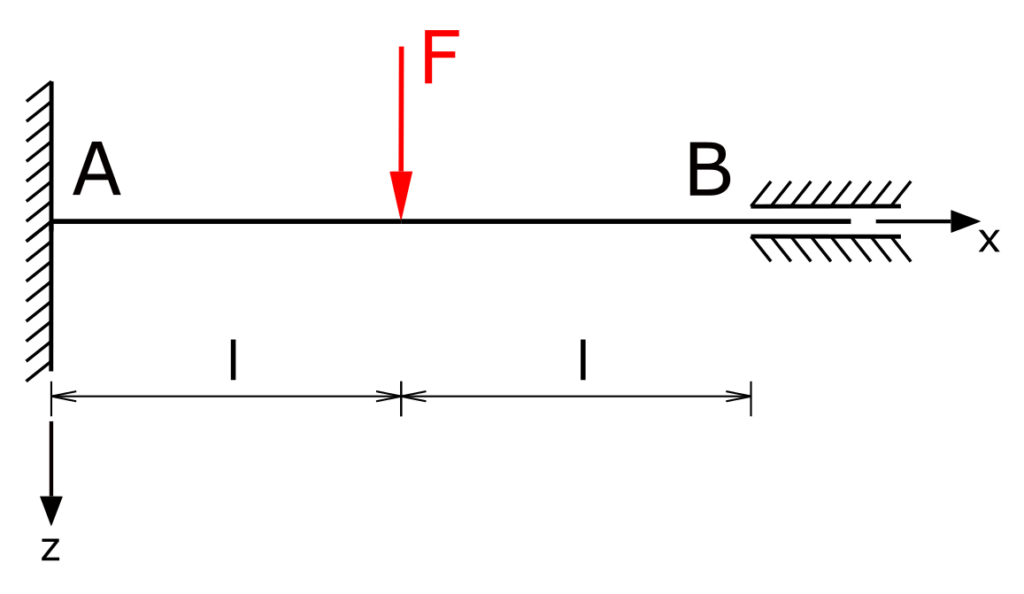
Ein Träger mit einer festen Einspannung A und einer Gleitführung B wird durch die Kraft F mittig belastet. Welche Lagerreaktionen treten auf?
Lösung
Im ersten Schritt werden die Gleichungen für die Lagerreaktionen ermittelt. Für die spätere Ermittlung der Schnittgrößen wird der Träger in zwei Bereiche eingeteilt. In den nachfolgenden Gleichungen werden die Horizontalkräfte nicht weiter betrachtet, da sie offensichtlich Null ist. Linksdrehende Momente sind positiv.
Ermittlung der Lagerreaktionen
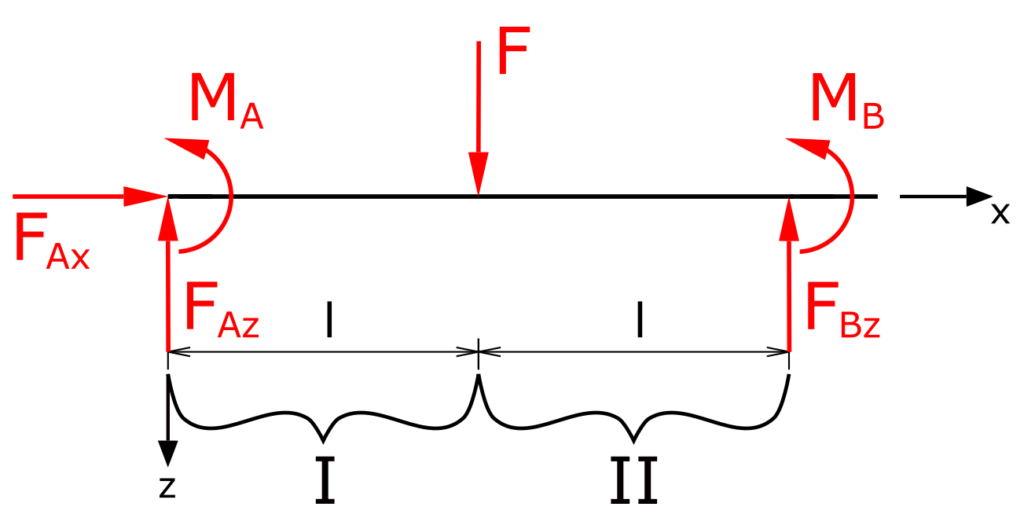
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{1} \sum F_z = 0 = -F_{Az} + F - F_{Bz} \]
Die Summe der der Momente um A
\[ \tag{2} \sum M(A) = 0 = M_A-F \cdot l+2 \cdot F_{Bz} \cdot l+M_B \]
Bei einem statisch überbestimmten Träger (bzw. statisch unbestimmten Träger) können die Lagerreaktionen allein aus diesen Gleichungen nicht ermittelt werden, da es zu viele Unbekannte gibt. Daher werden im nächsten Schritt die Funktionen der Biegemomente und der Biegelinien ermittelt.
Biegemomente
Biegemoment in Bereich I
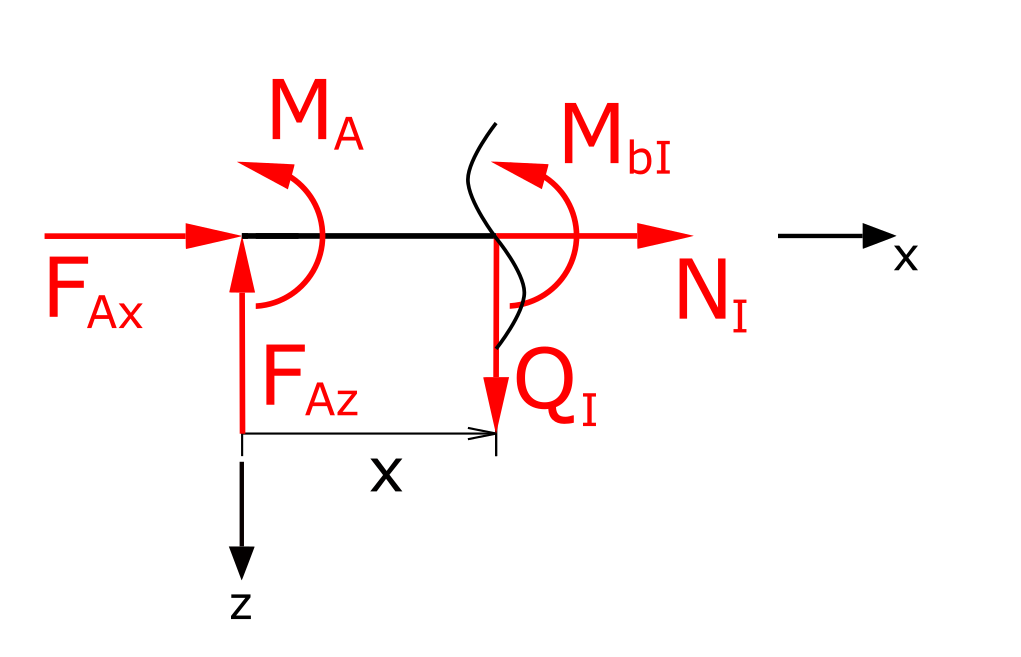
Die Summe der Momente um x liefert
\[ \tag{3} \sum M(x) = 0 = M_A + M_{bI}-F_{Az} \cdot x \]
\[ \tag{4} M_{bI} = F_{Az} \cdot x - M_A \]
Biegemoment in Bereich II
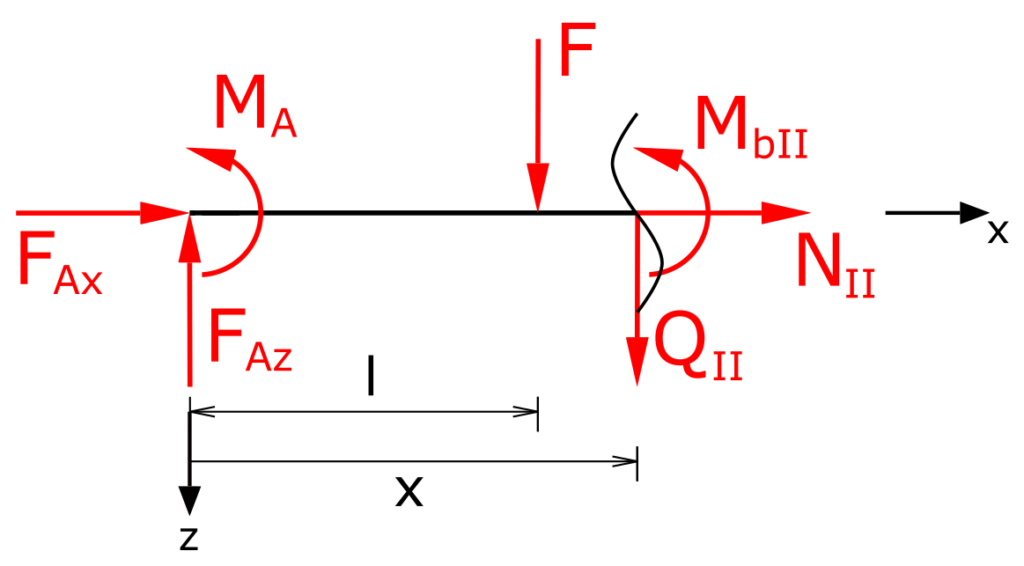
Die Summe der Momente um x liefert
\[ \tag{5} \sum M(x) = 0 = M_A - F_{Az} \cdot x+F \cdot (x-l)+M_{bII} \]
\[ \tag{6} M_{bII} = (F_{Az}-F) \cdot x+F \cdot l-M_A \]
Biegelinien
Die Biegelinie wird auf Basis der Bernoulli-Balkenbiegung bestimmt. Der grundsätzliche Zusammenhang lautet
\[ w'' = \frac{-M_b}{E \cdot I} \]
Dabei ist w'' die zweite Ableitung der Biegelinie, E der Elastizitätsmodul und I das Flächenträgheitsmoment. Die Biegelinie w erhält man durch zweifache Integration über x. Daraus folgt für den vorliegenden Fall
Biegelinie in Bereich I
\[ \tag{7} w''_1 = \frac{1}{E \cdot I} \cdot \left( M_A - F_{Az} \cdot x \right) \]
\[ \tag{8} w'_1 = \frac{1}{E \cdot I} \cdot \left( M_A \cdot x - \frac{1}{2} F_{Az} \cdot x^2 \right) + c_1 \]
\[ \tag{9} w_1 = \frac{1}{E \cdot I} \cdot \left( \frac{1}{2} M_A \cdot x^2 - \frac{1}{6} F_{Az} \cdot x^3 \right) + c_1 \cdot x + c_2 \]
Biegelinie in Bereich II
\[ \tag{10} w''_2 = \frac{1}{E \cdot I} \cdot \left( (F-F_{Az}) \cdot x - F \cdot l + M_A \right) \]
\[ \tag{11} w'_2 = \frac{1}{E \cdot I} \cdot \left( \frac{1}{2}(F-F_{Az}) \cdot x^2 - F \cdot l \cdot x + M_A \cdot x \right) + c_3 \]
\[ \tag{12} w_2 = \frac{\frac{1}{6}(F-F_{Az}) \cdot x^3 - \frac{1}{2} F \cdot l \cdot x^2 + \frac{1}{2} M_A \cdot x^2 }{E \cdot I} + c_3 \cdot x + c_4 \]
Als nächstes werden die Rand- und Übergangsbedingungen aufgestellt.
Rand- und Übergangsbedingungen
Die Durchbiegung an der Stelle x = 0 ist gleich Null
\[ \tag{13} w_1(x=0) = 0 = \frac{1}{E \cdot I} \cdot \left( \frac{1}{2} M_A \cdot 0^2 - \frac{1}{6} F_{Az} \cdot 0^3 \right) + c_1 \cdot 0 + c_2 \]
\[ \tag{14} c_2 = 0 \]
Die Durchbiegung an der Stelle x = 2l ist gleich Null
\[ \tag{15} w_2(x=2l) = 0 = \frac{ \frac{4}{3}(F-F_{Az}) \cdot l^3 - 2 F \cdot l^3 + 2 M_A \cdot l^2}{E \cdot I} + c_3 \cdot 2l + c_4 \]
Der Winkel an der Stelle x = 0 ist gleich Null
\[ \tag{16} w'_1(x=0) = 0 = \frac{1}{E \cdot I} \cdot \left( M_A \cdot 0 - \frac{1}{2} F_{Az} \cdot 0^2 \right) + c_1 \]
\[ \tag{17} c_1 = 0 \]
Der Winkel an der Stelle x = 2l ist gleich Null
\[ \tag{18} w'_2(x=2l) = 0 = \frac{1}{E \cdot I} \cdot \left( 2(F-F_{Az}) \cdot l^2 - F \cdot l^3 + 2M_A l \right) + c_3 \]
Die Durchbiegung beider Biegelinien an der Stelle x = l ist gleich groß
\[ \tag{19} \frac{\frac{1}{2} M_A \cdot l^2 - \frac{1}{6} F_{Az} \cdot l^3 }{E \cdot I} = \frac{ \frac{1}{6}(F-F_{Az}) \cdot l^3 - \frac{1}{2} F \cdot l^3 + \frac{1}{2} M_A \cdot l^2 }{E \cdot I} + c_3 \cdot l + c_4 \]
Der Winkel beider Biegelinien an der Stelle x = l ist gleich groß
\[ \tag{20} \frac{ M_A \cdot l - \frac{1}{2} F_{Az} \cdot l^2}{E \cdot I} = \frac{\frac{1}{2}(F-F_{Az}) \cdot l^2 - F \cdot l^2 + M_A \cdot l }{E \cdot I} + c_3\]
Die Gleichungen können nun aufgelöst werden. Die Integrationskonstanten ergeben sich zu
\[ \tag{21} c_3 = \frac{F \cdot l^2}{2 \cdot E \cdot I} \]
\[ \tag{22} c_4 = - \frac{F \cdot l^3}{6 \cdot E \cdot I} \]
Die Lagerreaktionen betragen
\[ \tag{23} M_A = \frac{F \cdot l}{4} \]
\[ \tag{24} M_B = - \frac{F \cdot l}{4} \]
\[ \tag{25} F_{Az} = \frac{F}{2} \]
\[ \tag{26} F_{Bz} = \frac{F}{2} \]
Der Vollständigkeit halber
\[ \tag{27} F_{Ax} = 0 \]
Damit sind die Lagerreaktionen für den statisch überbestimmten Träger ermittelt.
Werbung




