In this exercise, the support reactions for a statically indetermined beam are calculated using the bending line.
Exercise
A beam with a fixed restraint A and a sliding guide B is loaded centrally by the force F. Which bearing loads occur?
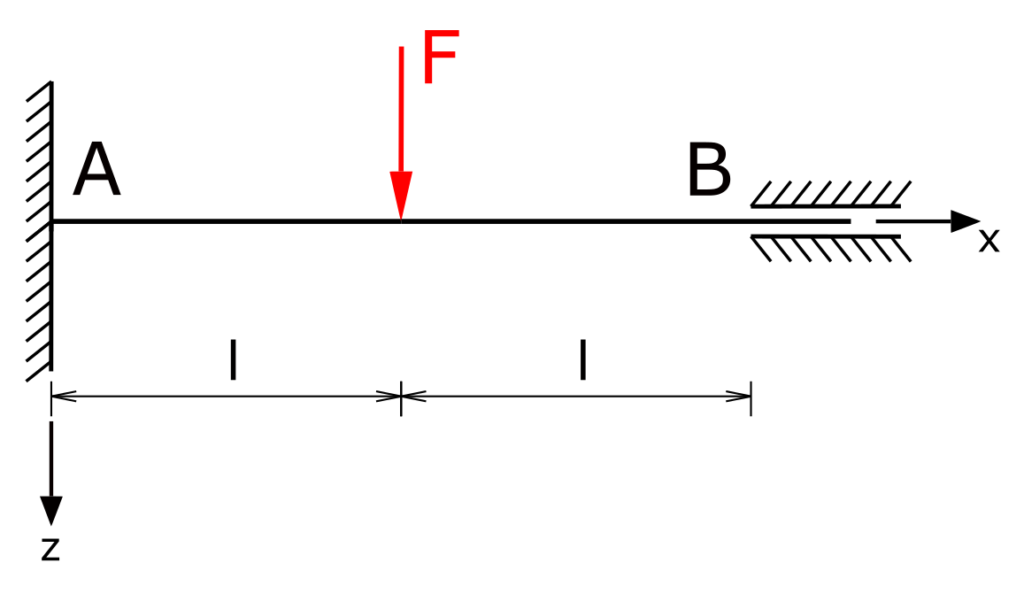
Solution
In the first step, the equations for the bearing reactions are determined. For the subsequent determination of the internal forces, the beam is divided into two areas. The horizontal forces are not considered further in the following equations, since they are obviously zero. Left turning moments are positive.
Bearing reactions
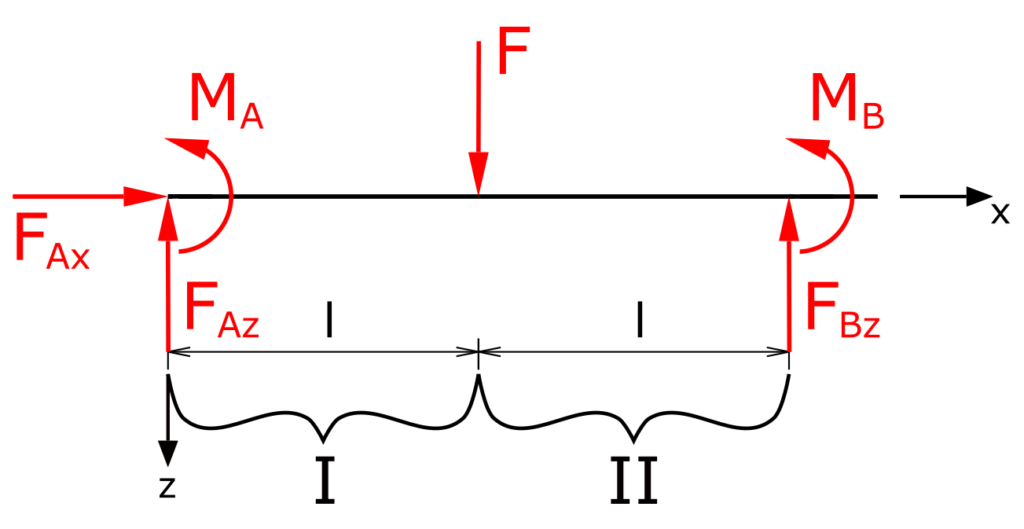
The sum of forces in z-direction is
\[ \tag{1} \sum F_z = 0 = -F_{Az} + F - F_{Bz} \]
The sum of moments regarding point A
\[ \tag{2} \sum M(A) = 0 = M_A-F \cdot l+2 \cdot F_{Bz} \cdot l+M_B \]
In the case of a statically indetermined beam, the bearing reactions cannot be determined from these equations alone, since there are too many unknowns. Therefore, in the next step, the functions of the bending moments and the bending lines are determined.
Bending moments
Bending moment in section I
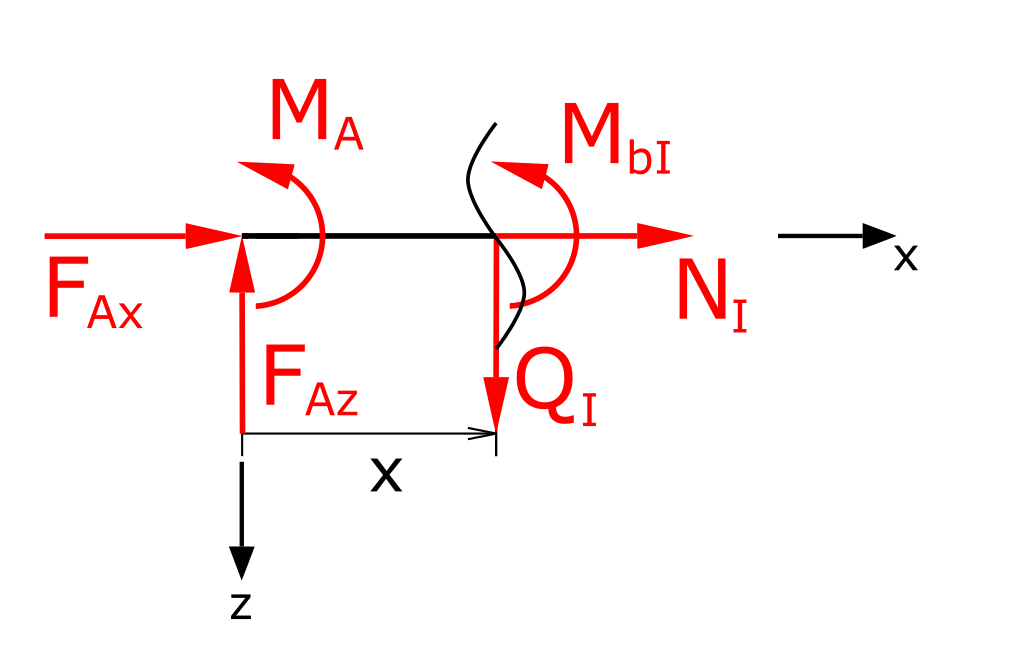
The sum of moments regarding x is
\[ \tag{3} \sum M(x) = 0 = M_A + M_{bI}-F_{Az} \cdot x \]
\[ \tag{4} M_{bI} = F_{Az} \cdot x - M_A \]
Bending moments in section II
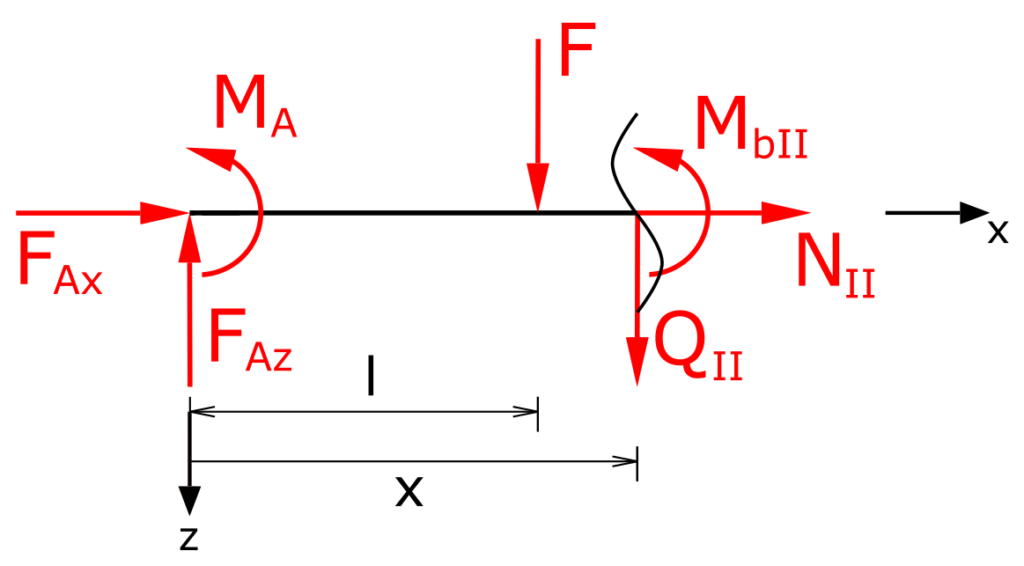
The sum of moments regarding x is
\[ \tag{5} \sum M(x) = 0 = M_A - F_{Az} \cdot x+F \cdot (x-l)+M_{bII} \]
\[ \tag{6} M_{bII} = (F_{Az}-F) \cdot x+F \cdot l-M_A \]
Deflection lines
The bending line is determined on the basis of the Bernoulli beam bending. The basic relation is
\[ w'' = \frac{-M_b}{E \cdot I} \]
Here w'' is the second derivative of the bending line, E is the (Young's) modulus of elasticity and I is the area moment of inertia. The bending line w is obtained by integrating twice over x. It follows from this for the present case
Bending line for section I
\[ \tag{7} w''_1 = \frac{1}{E \cdot I} \cdot \left( M_A - F_{Az} \cdot x \right) \]
\[ \tag{8} w'_1 = \frac{1}{E \cdot I} \cdot \left( M_A \cdot x - \frac{1}{2} F_{Az} \cdot x^2 \right) + c_1 \]
\[ \tag{9} w_1 = \frac{1}{E \cdot I} \cdot \left( \frac{1}{2} M_A \cdot x^2 - \frac{1}{6} F_{Az} \cdot x^3 \right) + c_1 \cdot x + c_2 \]
Bending line for section II
\[ \tag{10} w''_2 = \frac{1}{E \cdot I} \cdot \left( (F-F_{Az}) \cdot x - F \cdot l + M_A \right) \]
\[ \tag{11} w'_2 = \frac{1}{E \cdot I} \cdot \left( \frac{1}{2}(F-F_{Az}) \cdot x^2 - F \cdot l \cdot x + M_A \cdot x \right) + c_3 \]
\[ \tag{12} w_2 = \frac{\frac{1}{6}(F-F_{Az}) \cdot x^3 - \frac{1}{2} F \cdot l \cdot x^2 + \frac{1}{2} M_A \cdot x^2 }{E \cdot I} + c_3 \cdot x + c_4 \]
Next, the boundary and transition conditions are established.
Boundary and transition conditions
The deflection at the point x = 0 is equal to zero
\[ \tag{13} w_1(x=0) = 0 = \frac{1}{E \cdot I} \cdot \left( \frac{1}{2} M_A \cdot 0^2 - \frac{1}{6} F_{Az} \cdot 0^3 \right) + c_1 \cdot 0 + c_2 \]
\[ \tag{14} c_2 = 0 \]
The deflection at the point x = 2l is zero
\[ \tag{15} w_2(x=2l) = 0 = \frac{ \frac{4}{3}(F-F_{Az}) \cdot l^3 - 2 F \cdot l^3 + 2 M_A \cdot l^2}{E \cdot I} + c_3 \cdot 2l + c_4 \]
The angle at the point x = 0 is equal to zero
\[ \tag{16} w'_1(x=0) = 0 = \frac{1}{E \cdot I} \cdot \left( M_A \cdot 0 - \frac{1}{2} F_{Az} \cdot 0^2 \right) + c_1 \]
\[ \tag{17} c_1 = 0 \]
The angle at the point x = 2l is equal to zero
\[ \tag{18} w'_2(x=2l) = 0 = \frac{1}{E \cdot I} \cdot \left( 2(F-F_{Az}) \cdot l^2 - F \cdot l^3 + 2M_A l \right) + c_3 \]
The deflection of both bending lines at the point x = l is the same
\[ \tag{19} \frac{\frac{1}{2} M_A \cdot l^2 - \frac{1}{6} F_{Az} \cdot l^3 }{E \cdot I} = \frac{ \frac{1}{6}(F-F_{Az}) \cdot l^3 - \frac{1}{2} F \cdot l^3 + \frac{1}{2} M_A \cdot l^2 }{E \cdot I} + c_3 \cdot l + c_4 \]
The angle of both bending lines at the point x = l is the same
\[ \tag{20} \frac{ M_A \cdot l - \frac{1}{2} F_{Az} \cdot l^2}{E \cdot I} = \frac{\frac{1}{2}(F-F_{Az}) \cdot l^2 - F \cdot l^2 + M_A \cdot l }{E \cdot I} + c_3\]
The equations can now be solved. The constants of integration are given by
\[ \tag{21} c_3 = \frac{F \cdot l^2}{2 \cdot E \cdot I} \]
\[ \tag{22} c_4 = - \frac{F \cdot l^3}{6 \cdot E \cdot I} \]
The bearing loads are
\[ \tag{23} M_A = \frac{F \cdot l}{4} \]
\[ \tag{24} M_B = - \frac{F \cdot l}{4} \]
\[ \tag{25} F_{Az} = \frac{F}{2} \]
\[ \tag{26} F_{Bz} = \frac{F}{2} \]
And for the sake of completeness
\[ \tag{27} F_{Ax} = 0 \]
The bearing reactions for the statically indetermined beam are thus determined.

