Werbung
In dieser Übung werden folgende Fragen beantwortet:
- Wie berechnet man eine resultierende Kraft aus mehreren Kräften in einem zentralen ebenen Kräftesystem?
- Wie zerlegt man eine Kraft in ihre Komponenten?
- Wann benutzt man Sinus und wann Kosinus?
- Wie berechnet man den Winkel einer resultierenden Kraft?
- Wie kann man die resultierende Kraft grafisch bestimmen?
Hier gibt es einen Onlinerechner zur Berechnung der resultierenden Kraft.
Aufgabe
Auf einen Leitungsmast wirken mehrere Kräfte in der horizontalen Ebene. Es ist die resultierende Kraft der 4 Kräfte für die folgenden Parameter zu berechnen.
F1 = 1.000 N, α = 45°F2 = 800 N, β = 20°
F3 = 1.500 N, γ = 30°
F4 = 900 N, δ = 15°
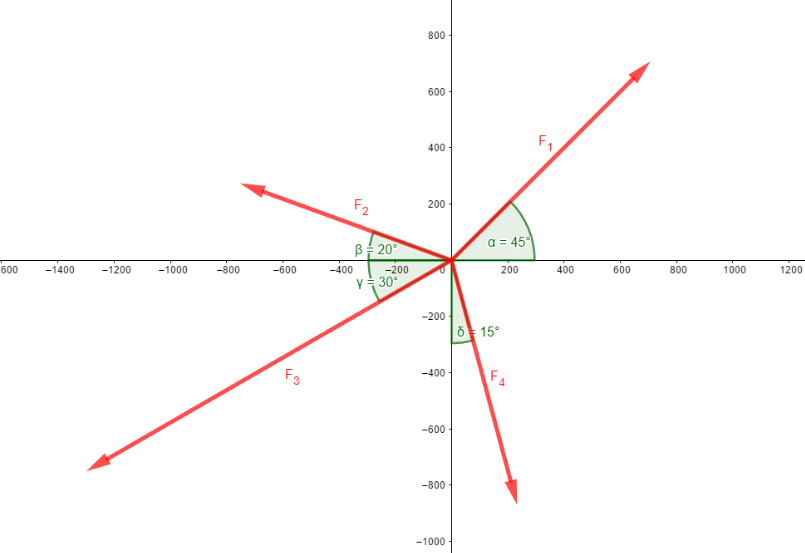
Lösung
Resultierende Kraft berechnen
Die resultierende Kraft wird hier FR genannt, die Komponenten FRx und FRy. Der Winkel der resultierenden Kraft ist ε.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Die Summe der Kräfte in x-Richtung entspricht der x-Komponente der resultierenden Kraft.
\[\tag{1} {F_{\mathit{Rx}}}={F_4} \sin{\left( \delta \right) }-{F_3} \cos{\left( \gamma \right) }-{F_2} \cos{\left( \beta \right) }+{F_1} \cos{\left( \alpha \right) }\]
Die Summe der Kräfte in y-Richtung entspricht der y-Komponente der resultierenden Kraft.
\[\tag{2} {F_{\mathit{Ry}}}=-{F_4} \cos{\left( \delta \right) }-{F_3} \sin{\left( \gamma \right) }+{F_2} \sin{\left( \beta \right) }+{F_1} \sin{\left( \alpha \right) }\]
Der Betrag der resultierenden Kraft wird mit dem Satz des Pythagoras ausgerechnet.
\[\tag{3} {F_R}=\sqrt{{{{F_{\mathit{Ry}}}}^{2}}+{{{F_{\mathit{Rx}}}}^{2}}}\]
Der Winkel der resultierenden Kraft zur x-Achse ergibt sich aus
\[\tag{4} \epsilon =\operatorname{atan}\left( \frac{{F_{\mathit{Ry}}}}{{F_{\mathit{Rx}}}}\right) \]
Mit den eingesetzten Zahlen ergeben sich dann folgende Werte:
\[\tag{5} {F_{\mathit{Rx}}}=-1110.7 N\]
\[\tag{6} {F_{\mathit{Ry}}}=-638.6 N\]
\[\tag{7} {F_{\mathit{R}}}=1.281 N\]
\[\tag{8} \epsilon =29.9°\]
Es gibt eine Alternative zur Berechnung der Resultierenden, die auch für mehrere Kräfte funktioniert:
Resultierende Kraft zeichnerisch ermitteln
Diese Vorgehensweise wird auch Seileck-Verfahren genannt.
Die einzelnen Kräfte sind hierbei maßstäblich (!) zu zeichnen. Am einfachsten ist es, die Kräfte wie hier gezeigt, ausgehend vom Ursprung des Koordinatensystems zu zeichnen und anschließend parallel zu verschieben. Die Reihenfolge der Verschiebung ist egal, wichtig ist nur, dass am Ende eine "Kette" aller Kräfte entsteht. Die resultierende Kraft erhält man, indem man den Ursprung des Koordinatensystems mit dem Ende der Kette verbindet.
Das nachfolgende Bild entspricht den o.a. 4 Kräften F1 bis F4, diesmal präzise und maßstäblich dargestellt. Die schwarzen Pfeile sind die jeweils parallel verschobenen Kraftvektoren, der blaue Vektor ist die resultierende Kraft.
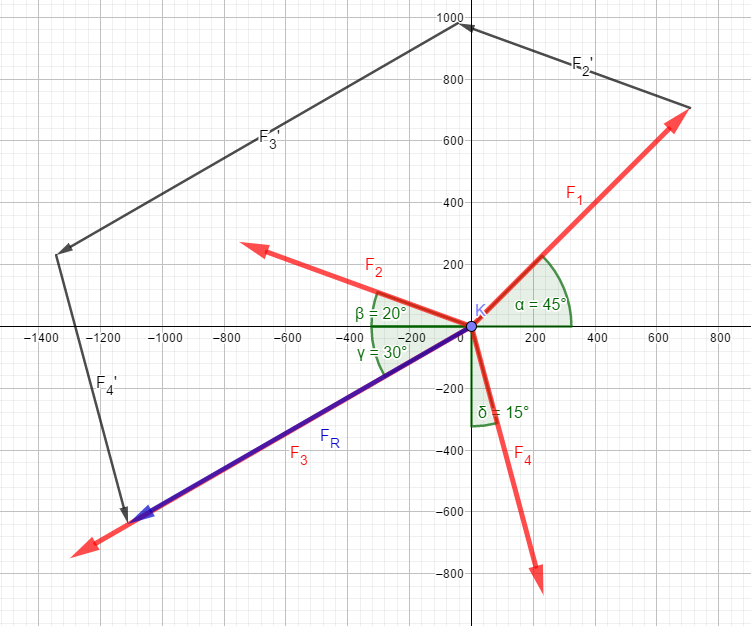
Hier gibt es weitere interessante Aufgaben zum Thema resultierende Kraft.
Werbung




