Werbung
Diese Aufgabe behandelt folgende Fragen:
- Welche Kräfte kann ein Gelenk übertragen?
- Wie berechnet man die Lagerreaktionen eines Trägers mit Gelenk?
Hier gibt es eine Übersicht über Lagerarten, Gelenke und Führungen und deren Reaktionskräfte.
Aufgabe
Ein Träger ist einseitig fest eingespannt und über ein Gelenk mit einem Loslager verbunden. Es sollen die Lagerreaktionen in der festen Einspannung A, dem Gelenk B und im Loslager C bestimmt werden.
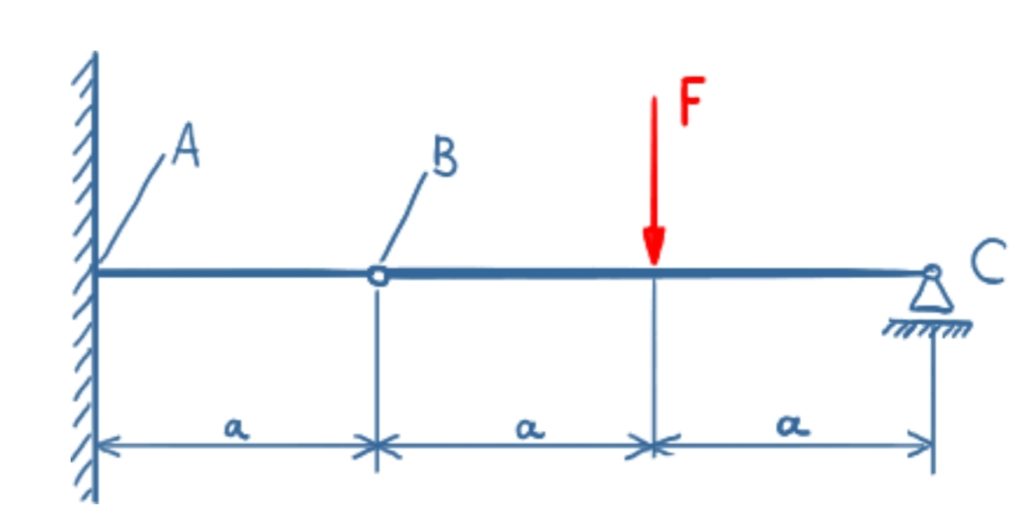
Lösung
Der Träger wird in zwei Bereiche eingeteilt.
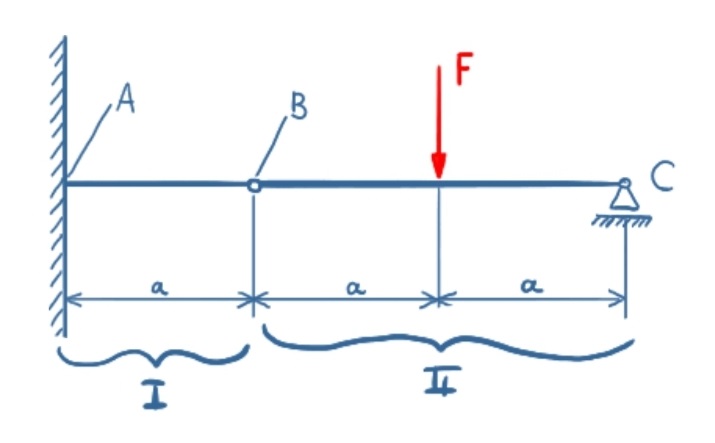
Anschließend werden die Bereiche freigeschnitten und die Lagerkräfte und Gelenkkräfte angetragen. Zu beachten ist, dass die Gelenkkräfte in den beiden unterschiedlichen Bereichen entgegengesetzt angetragen werden.
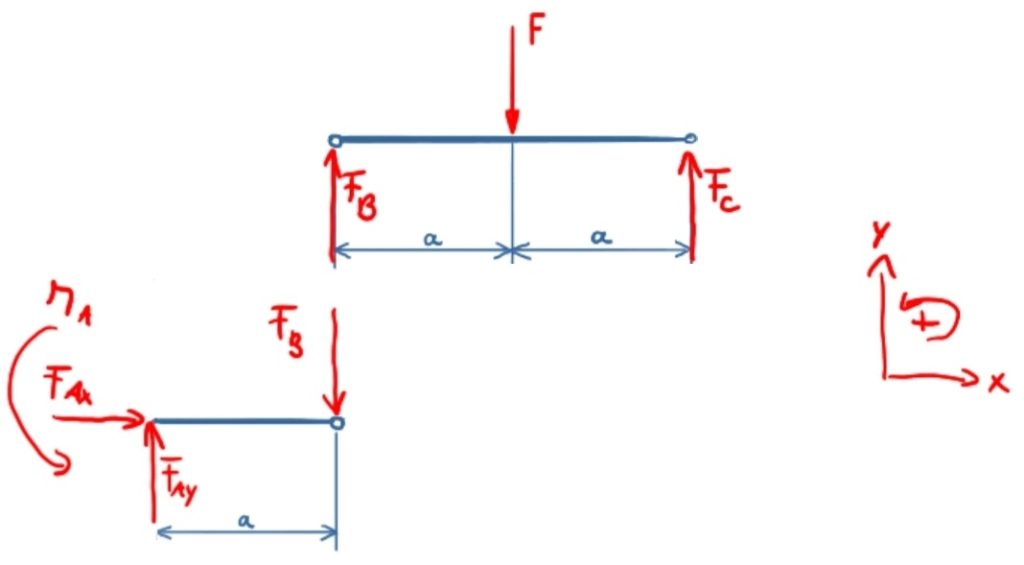
Die Bilanzen bzw. Kräfte- und Momentengleichgewichte werden für beide Bereiche separat aufgestellt.
Bereich I:
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{1} \sum F_x = 0 = F_{Ax} \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{2} \sum F_y = 0 = F_{Ay} - F_B \]
Das Momentengleichgewicht um Punkt A ist
\[\tag{3} \sum M(A) = 0 = M_A - F_B \cdot a \]
Bereich II:
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{4} \sum F_x = 0 \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{5} \sum F_y = 0 = F_B - F + F_C \]
Das Momentengleichgewicht um Punkt B liefert
\[\tag{6} \sum M(B) = 0 = - F \cdot a + F_C \cdot 2 \cdot a \]
\[\tag{7} F_C = \frac{F \cdot \bcancel{a}}{2\bcancel{a}} \]
Einsetzen und Auflösen
Damit folgt aus Gleichung 5 für FB
\[\tag{8} F_B = \frac{F}{2} \]
Gleichung 2 liefert
\[\tag{9} F_{Ay} = \frac{F}{2} \]
Das Moment in der festen Einspannung ergibt sich aus Gleichung 3:
\[\tag{10} M_A = \frac{F \cdot a}{2} \]
Werbung




