Werbung
In dieser Übung werden die Reaktionskräfte auf der geneigten Ebene ermittelt.
Aufgabe
Ein Eisenbahnwaggon steht auf einer abschüssigen Strecke an einem (reibungsfreien) Prellbock. Welche Reaktionskräfte treten an den Rädern und am Prellbock auf?
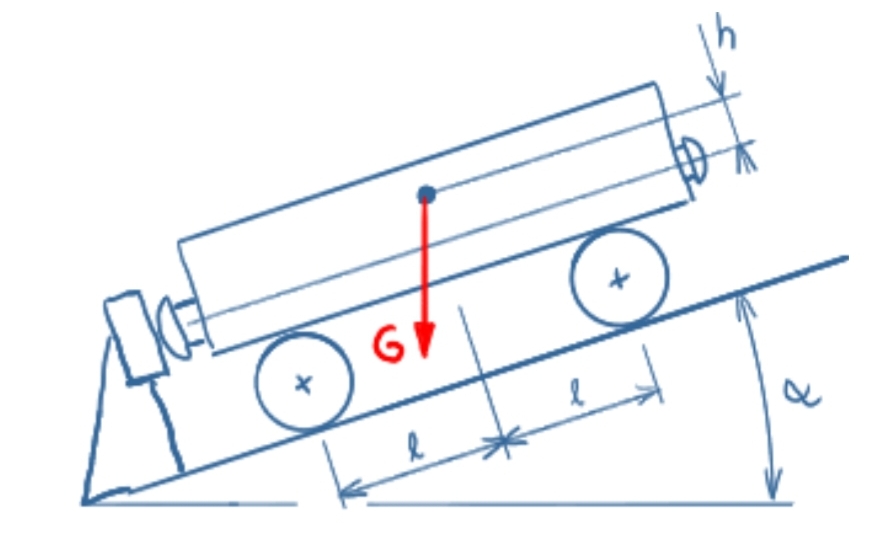
Lösung
Lösungsskizze
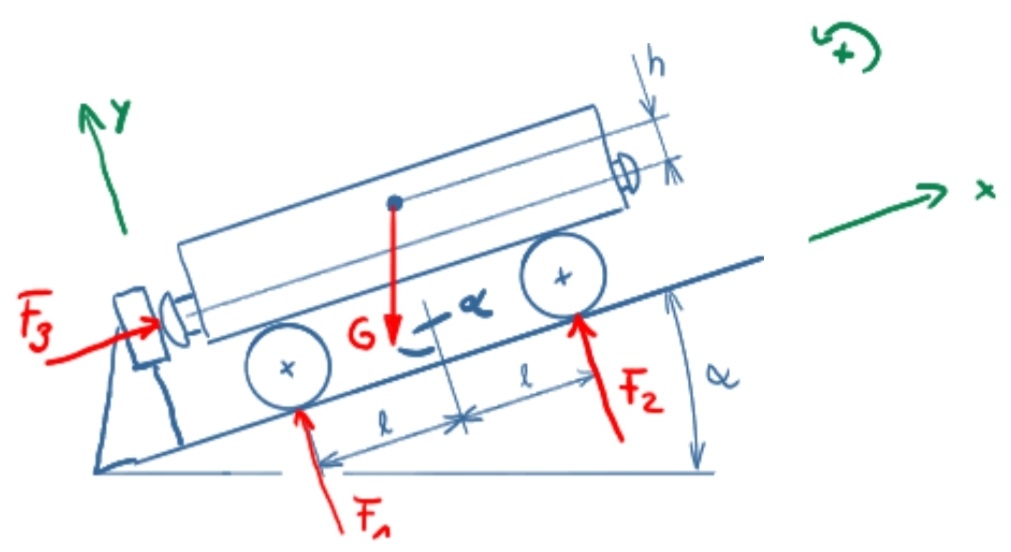
Lösungsweg
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]Das Koordinatensystem wird zur Lösung der Aufgabe um den Winkel α gedreht. Ohne Drehung des Koordinatensystems wäre die Berechnung auch möglich, allerdings wesentlich komplizierter, da dann in allen Kräften Winkelfunktionen vorkommen würden. Linksdrehende Momente sind positiv.
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{1} \sum F_x = 0 = F_3 - G \cdot \sin \alpha \]
\[\tag{2} F_3 = G \cdot \sin \alpha \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{3} \sum F_y = 0 = F_1 - G \cdot \cos \alpha + F_2 \]
Das Momentengleichgewicht kann aufgrund der geometrischen Vorgaben nur um G betrachtet werden und führt zu
\[\tag{4} \sum M(G) = 0 = F_3 \cdot h - F_1 \cdot l + F_2 \cdot l \]
\[\tag{5} 0 = G \cdot \sin \alpha \cdot h - F_1 \cdot l + F_2 \cdot l \]
\[\tag{6} F_2 = \frac{F_1 \cdot l - G \cdot \sin \alpha \cdot h}{l} \]
Aus Gleichung 3 ergibt sich damit
\[\tag{7} 0 = F_1 - G \cdot \cos \alpha + \frac{F_1 \cdot l - G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{8} G \cdot \cos \alpha = F_1 + \frac{F_1 \ \cdot \bcancel{l}}{\bcancel{l}} - \frac{G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{9} F_1 = \frac{G}{2} \cdot \left( \cos \alpha + \frac{\sin \alpha \cdot h}{l} \right) \]
F2 folgt aus Gleichung 6
\[\tag{10} F_2 = \frac{\frac{G}{2} \cdot \left( \cos \alpha + \frac{\sin \alpha \cdot h}{l} \right) \cdot l - G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{11} F_2 = \frac{ \frac{G}{2} \cdot \cos \alpha \cdot l + \frac{G}{2} \cdot \frac{\sin \alpha \cdot h}{\bcancel{l}} \cdot \bcancel{l} - G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{12} F_2 = \frac{ G \cdot \cos \alpha \cdot l - G \cdot \sin \alpha \cdot h}{2 \cdot l} \]
Damit sind die Reaktionskräfte auf der geneigten Ebene ermittelt.
Die Annahme, dass linksdrehende Momente positiv sind, folgt übrigens aus der sogenannten Rechte-Hand- bzw. Rechter-Daumen-Regel. Die Regel lautet: man betrachtet seine rechte Hand mit ausgestrecktem Daumen und gekrümmten Fingern. Der Daumen repräsentiert die Koordinatenachse und die Finger zeigen den positiven Drehsinn an.
Eine vergleichbare Aufgabe ist die Berechnung der Reaktionskräfte für ein Auto am Hang, das mit angezogener Handbremse geparkt wurde.
Werbung




