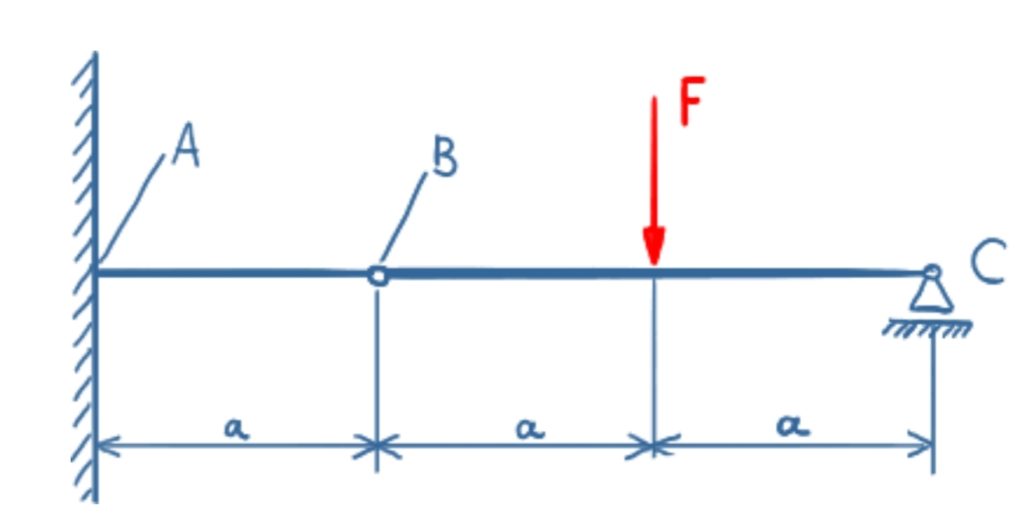
Task
Determine the bearing reactions in the fixed restraint A, the forces in joint B and the bearing reactions in the floating bearing C for the beam with the load F as shown.
Solution
The following video is in german language, but English subtitles are available.
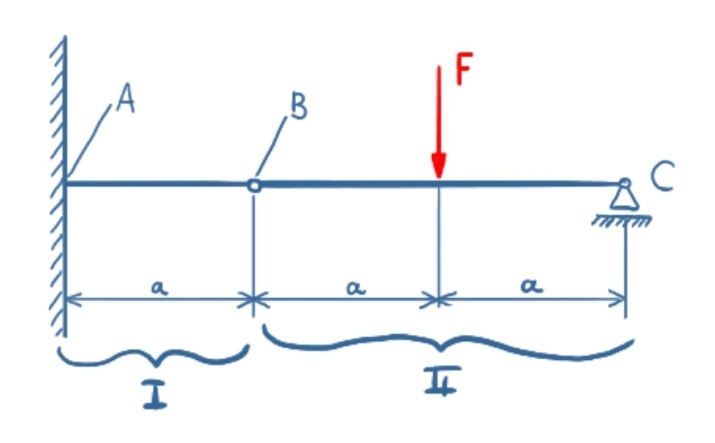
The beam has to be divided into two sections.
Then the sections are cut free and the bearing forces and joint forces applied. It should be noted that the joint forces are applied in opposite directions in the two different sections.
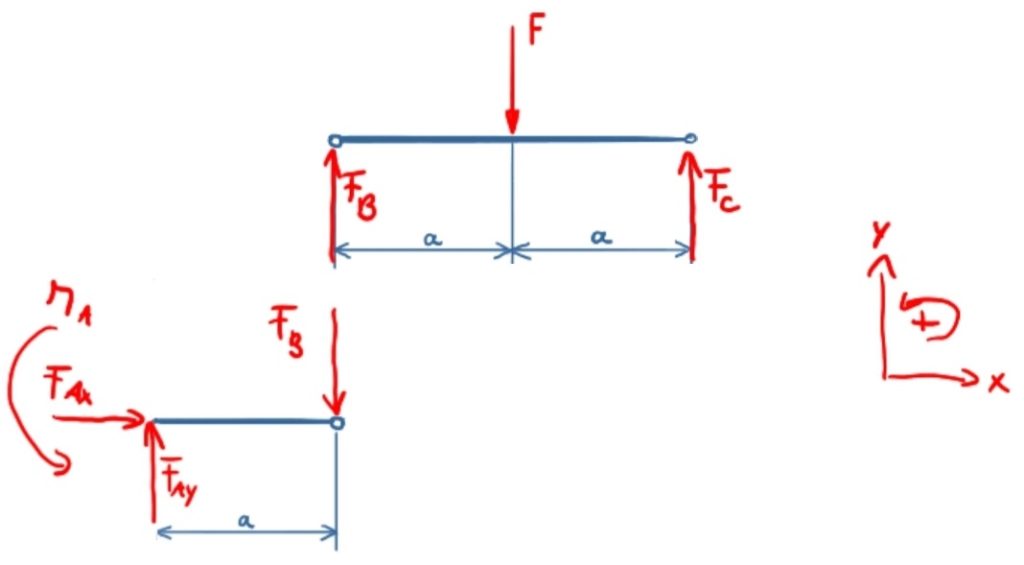
The balances or equilibria of forces and moments are set up separately for both areas.
Section I:
The equilibrium of forces in the x-direction is
\[\tag{1} \sum F_x = 0 = F_{Ax} \]
The equilibrium of forces in the y-direction is
\[\tag{2} \sum F_y = 0 = F_{Ay} - F_B \]
The equilibrium of moments around point A is
\[\tag{3} \sum M(A) = 0 = M_A - F_B \cdot a \]
Section II:
The equilibrium of forces in the x-direction is
\[\tag{4} \sum F_x = 0 \]
The equilibrium of forces in the y-direction is
\[\tag{5} \sum F_y = 0 = F_B - F + F_C \]
The equilibrium of moments around point B delivers
\[\tag{6} \sum M(B) = 0 = - F \cdot a + F_C \cdot 2 \cdot a \]
\[\tag{7} F_C = \frac{F \cdot \bcancel{a}}{2\bcancel{a}} \]
Substitute and solve
It follows from equation 5 for F B
\[\tag{8} F_B = \frac{F}{2} \]
Equation 2 yields
\[\tag{9} F_{Ay} = \frac{F}{2} \]
The moment in the fixed restraint results from equation 3:
\[\tag{10} M_A = \frac{F \cdot a}{2} \]

