Werbung
Aufgabe
Eine Klappbrücke mit der Eigengewichtskraft G wird durch ein Seil gehalten. Das Seil wird über eine Rolle umgelenkt.
Wie groß ist die Seilkraft in Abhängigkeit vom Öffnungswinkel der Klappbrücke?
Wann wird die Seilkraft obsolet?
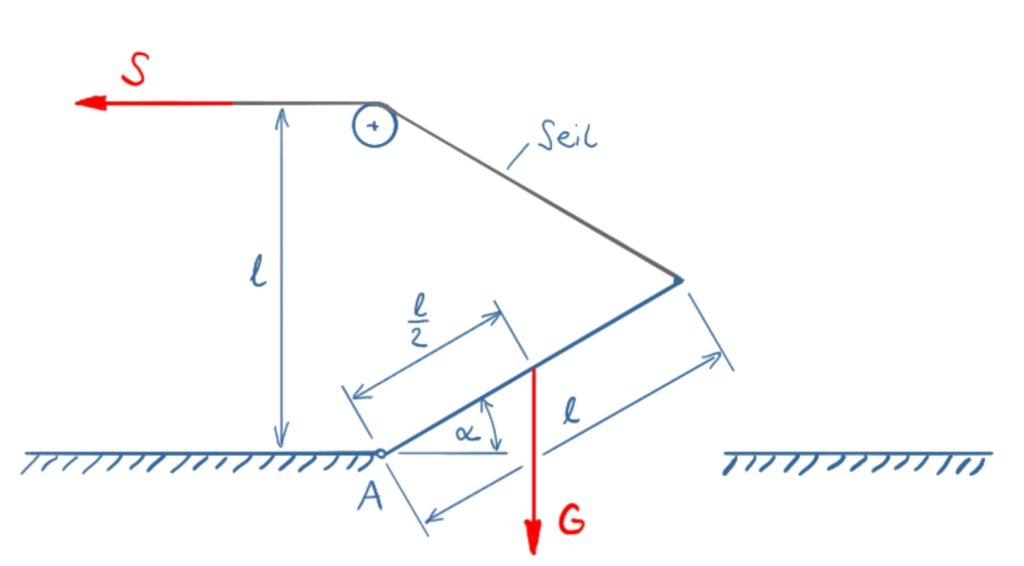
Lösung
Die Lösung beginnt mit dem Freischneiden des Systems und dem Antragen der Reaktionskräfte.
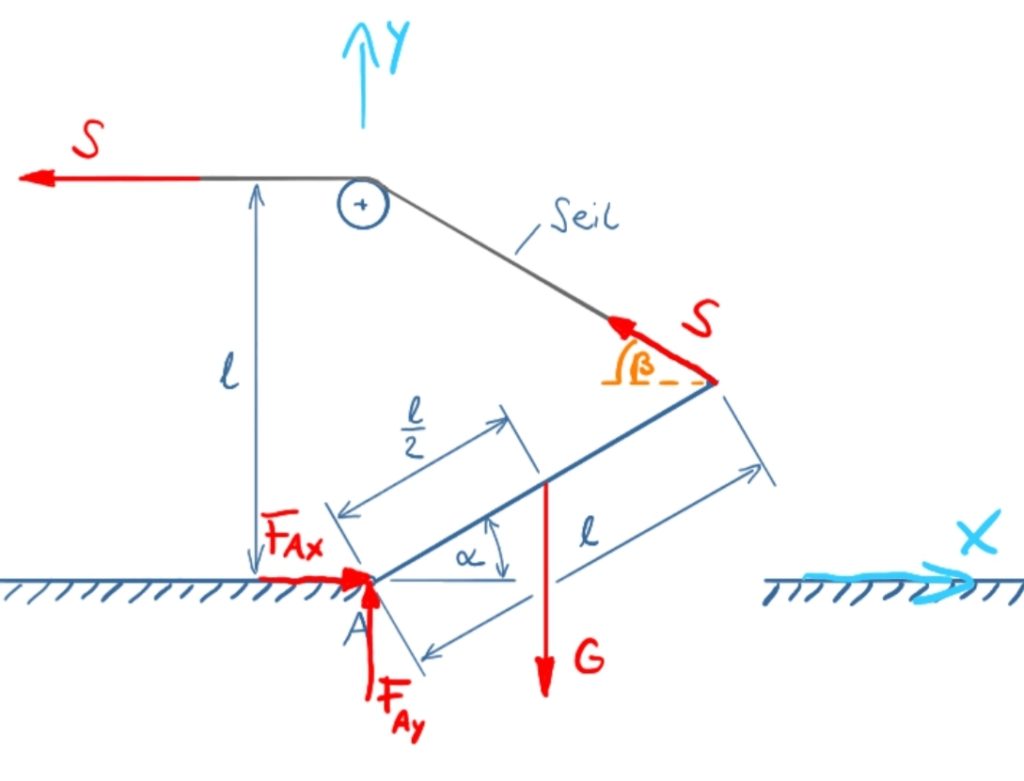
Um die Richtung der Seilkraft S in die Kräfte- und Momentenbilanzen einfließen zu lassen, wird der Winkel β eingeführt. Damit ergibt sich für
\[ \tag{1} \sum F_x = 0 = F_{Ax} - S \cdot \cos \beta \]
\[ \tag{2} \sum F_y = 0 = F_{Ay} - G + S \cdot \sin \beta \]
Aus der Momentenbilanz kann S bestimmt werden.
\[ \tag{3} \sum M(A) = 0 = -G \cdot \frac{l}{2} \cdot \cos \alpha + S \cdot l \cdot \cos \beta \cdot \sin \alpha + S \cdot l \cdot \sin \beta \cdot \cos \alpha \]
\[ \tag{4} G \cdot \frac{\bcancel{l}}{2} \cdot \cos \alpha = S \cdot \bcancel{l} \cdot \left( \cos \beta \cdot \sin \alpha + \sin \beta \cdot \cos \alpha \right) \]
\[ \tag{5} S = \frac{G \cdot \cos \alpha}{2 \cdot \left( \cos \beta \cdot \sin \alpha + \sin \beta \cdot \cos \alpha \right) } \]
Dabei lässt sich Winkelfunktionen zu α und β weiter vereinfachen, so dass sich folgende Funktion ergibt:
\[ \tag{6} S = \frac{G \cdot \cos \alpha}{2 \cdot \sin \left( \alpha + \beta \right) } \]
Der Winkel β lässt sich wie folgt beschreiben:
\[ \tag{7} \beta = arctan \left( \frac{\bcancel{l}1 - \bcancel{l} \cdot \sin \alpha}{\bcancel{l} \cdot \cos \alpha} \right) \]
Die gesuchte Funktion S(α) lautet:
\[ \tag{8} S(\alpha) = \frac{G \cdot \cos \alpha}{2 \cdot \sin \left( \alpha + arctan \left( \frac{1 - \sin \alpha}{\cos \alpha} \right) \right) } \]
Wann wird die Seilkraft obsolet?
Die Funktion ergibt Null, wenn der Zähler Null ergibt. Dies ist bei einem Winkel α von 90° der Fall, d.h. dort ist die Seilkraft dann obsolet.
Werbung




