Werbung
Diese Übung behandelt eine Bandbremse mit einem einfach wirkenden Betätigungshebel. Hier gibt es eine Übung zur Berechnung einer Bandbremse mit einem doppelt wirkenden Hebel.
Folgende Fragen werden behandelt:
- Wie berechnet man das Haltemoment einer Bandbremse?
- Unterscheidet sich das Haltemoment in beiden Drehrichtungen?
- In welcher Richtung funktioniert die Bremse besser?
Hier gibt es eine Übersichtstabelle mit Haft- und Gleitreibungswerten.
Aufgabe
Die dargestellte Bandbremse soll im Rechtslauf und Linkslauf betrieben werden. Wie groß kann das Haltemoment im Rechts- und Linkslauf maximal werden, ohne dass sich die Bremstrommel dreht?
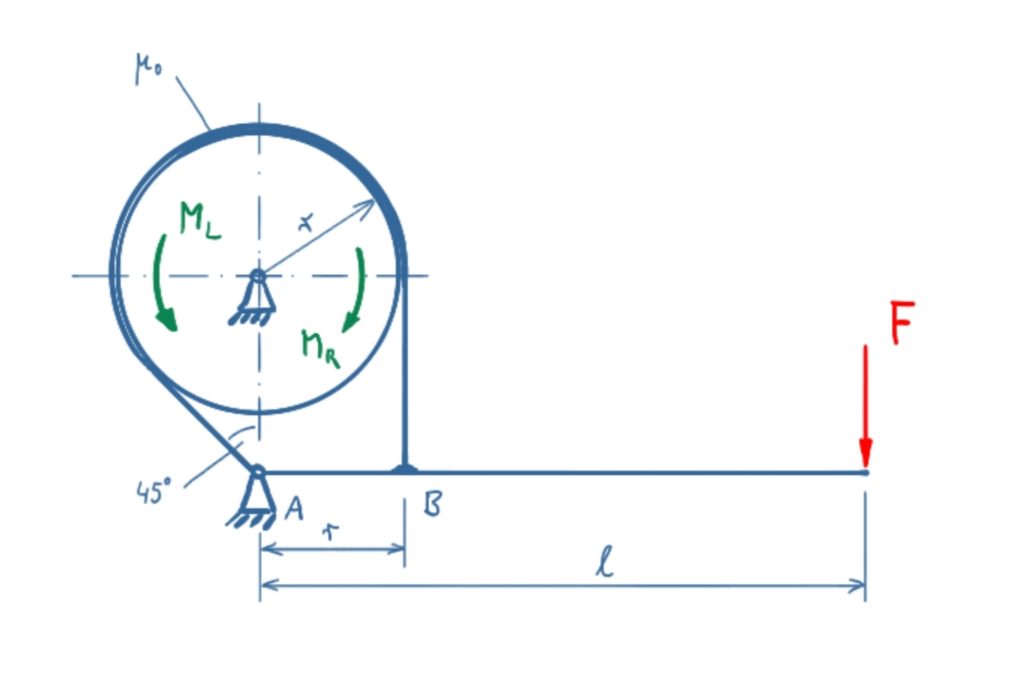
Lösung
Im ersten Schritt wird der Betätigungshebel freigeschnitten.
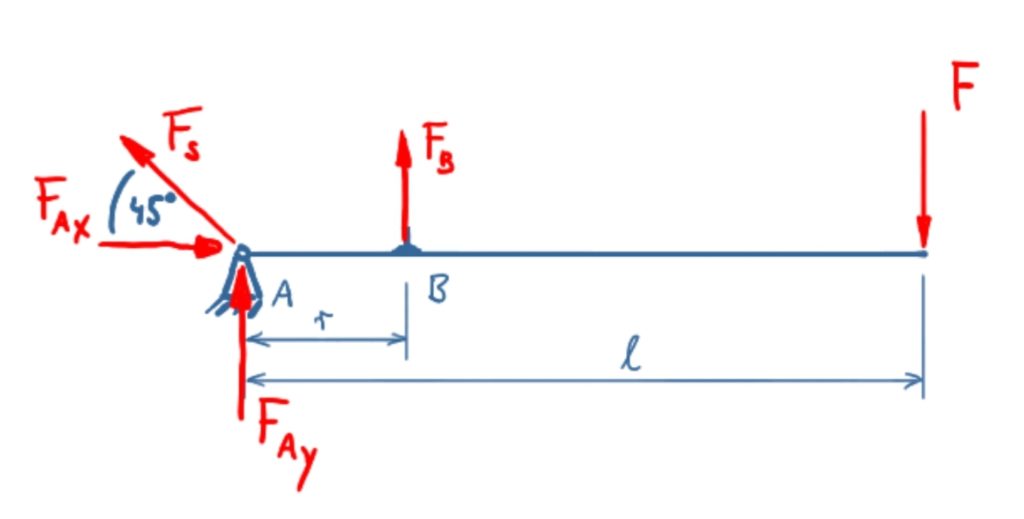
Die Kraft FS ist hier mit abgetragen, hat aber keinen Effekt auf den Betätigungshebel. In anderen Varianten dieser Aufgabe kann diese Kraft auch an einem separaten Lager abgetragen werden, d.h. das Band der Bandbremse ist dann an anderer Stelle befestigt.
\[ \require{cancel} \]Das Kräftegleichgewicht in x-Richtung lautet
\[ \tag{1} \sum F_x = 0 = F_{Ax} - F_S \cdot \cos 45° \]
Das Kräftegleichgewicht in y-Richtung lautet
\[ \tag{2} \sum F_y = 0 = F_{Ay} + F_S \cdot \sin 45° + F_B - F \]
Beide Kräftegleichgewichte liefern keine sinnvollen Informationen, aber das Momentengleichgewicht um A ergibt
\[ \tag{3} \sum M(A) = 0 = F_B \cdot r - F \cdot l \]
\[ \tag{4} F_B = \frac{F \cdot l}{r} \]
Als nächstes wird über die Seilreibungsformel (Euler-Eytelwein) der Zusammenhang zwischen Seilkraft FS und Bremskraft FB notiert. Dies erfolgt separat für die beiden unterschiedlichen Drehrichtungen.
Rechtslauf
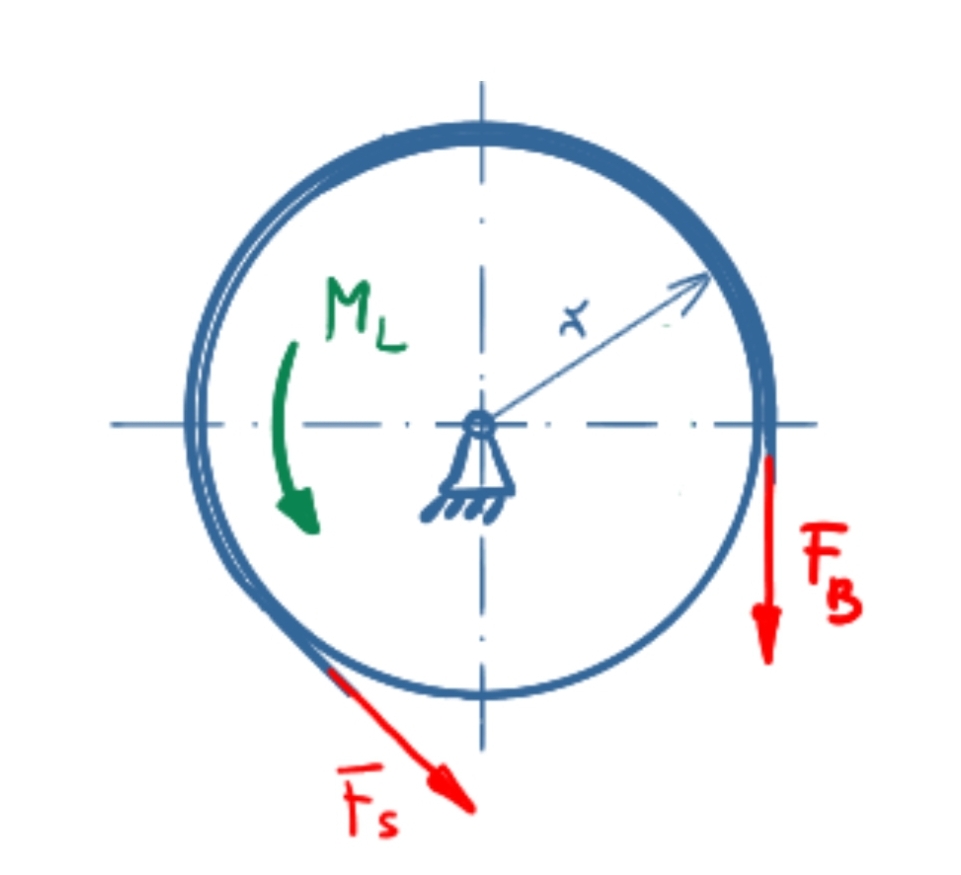
Beim linksdrehenden Moment liegt FB im auflaufenden Trum, FS im ablaufenden Trum. Es gilt also:
\[ \tag{5} F_B \leq F_S \cdot e^{µ \cdot \alpha} \]
\[ \tag{6} F_S \geq F_B \cdot e^{-µ \cdot \alpha} \]
In Verbindung mit dem Momentengleichgewicht um den Trommeldrehpunkt folgt daraus:
\[ \tag{7} \sum M = 0 = F_S \cdot r + M_L - F_B \cdot r \]
\[ \tag{8} M_L = F_B \cdot r - F_S \cdot r \]
\[ \tag{9} M_L = \frac{F \cdot l}{\bcancel{r}} \cdot \bcancel{r} - \frac{F \cdot l}{\bcancel{r}} \cdot e^{-µ \cdot \alpha} \cdot \bcancel{r}\]
\[ \tag{10} M_L = F \cdot l \cdot \left( 1 - e^{-µ \cdot \alpha} \right) \]
Linkslauf
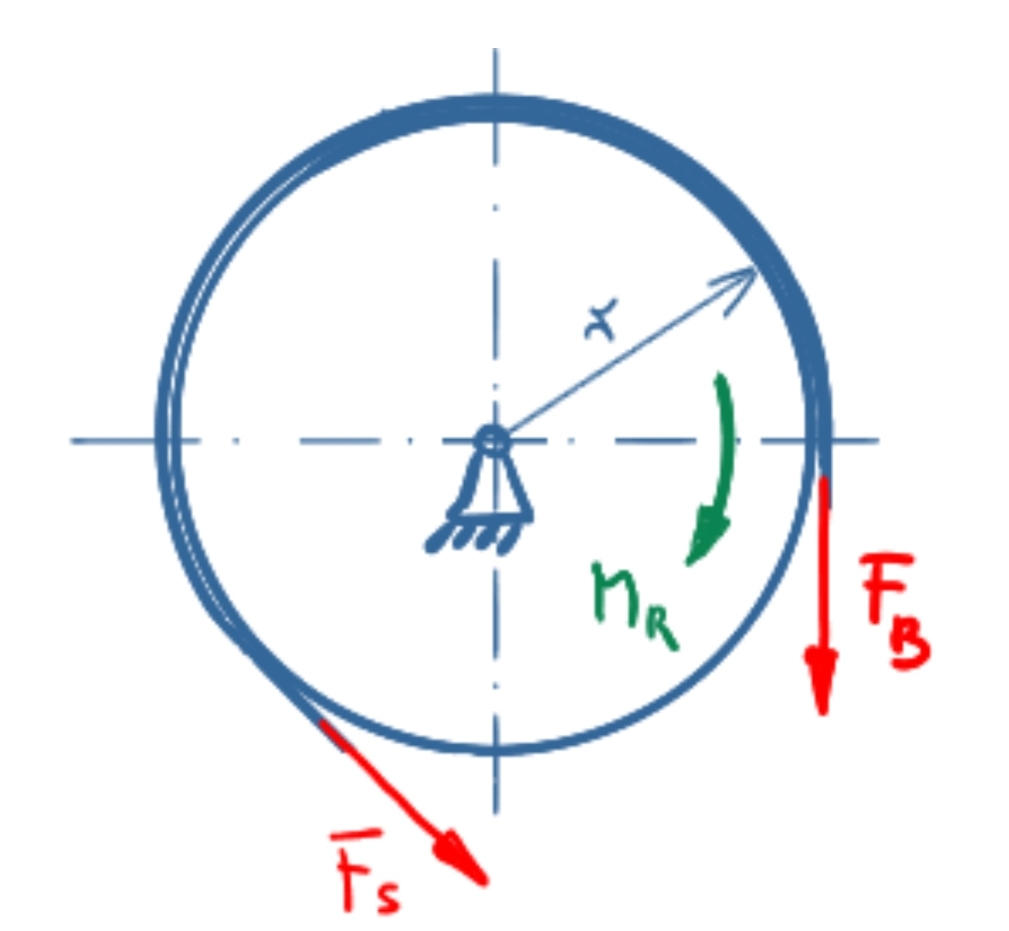
Beim rechtsdrehenden Moment liegt FB im ablaufenden Trum, FS im auflaufenden Trum. Es gilt also:
\[ \tag{11} F_S \leq F_B \cdot e^{µ \cdot \alpha} \]
In Verbindung mit dem Momentengleichgewicht um den Trommeldrehpunkt folgt daraus:
\[ \tag{12} \sum M = 0 = F_S \cdot r - M_R - F_B \cdot r \]
\[ \tag{13} M_R = F_S \cdot r - F_B \cdot r \]
\[ \tag{14} M_R = \frac{F \cdot l}{\bcancel{r}} \cdot e^{µ \cdot \alpha} \cdot \bcancel{r} - \frac{F \cdot l}{\bcancel{r}} \cdot \bcancel{r} \]
\[ \tag{15} M_R = F \cdot l \cdot \left(e^{µ \cdot \alpha} - 1 \right) \]
Damit ist gezeigt, dass die hier berechnete Bandbremse im Linkslauf ein erheblich höheres Haltemoment hat als im Rechtslauf.
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Reibung.
Werbung




