Werbung
Diese Übung zeigt die Anwendung der Seilreibungsformel. Hier gibt es einen Onlinerechner für die Seilreibung.
Aufgabe
Ein Riemen treibt mit einer Kraft A = 890 N im Lasttrum und einem Umschlingungswinkel α = 160° eine Rolle an. Der Haftreibungskoeffizient beträgt µ0 = 0,3.
a) Wie groß ist die Kraft L im Leertrum?
b) Wie groß muss der Umschlingungswinkel α' sein, wenn bei gleichbleibender Kraft L im Leertrum die Kraft im Lasttrum auf A' = 1.100 N erhöht wird?
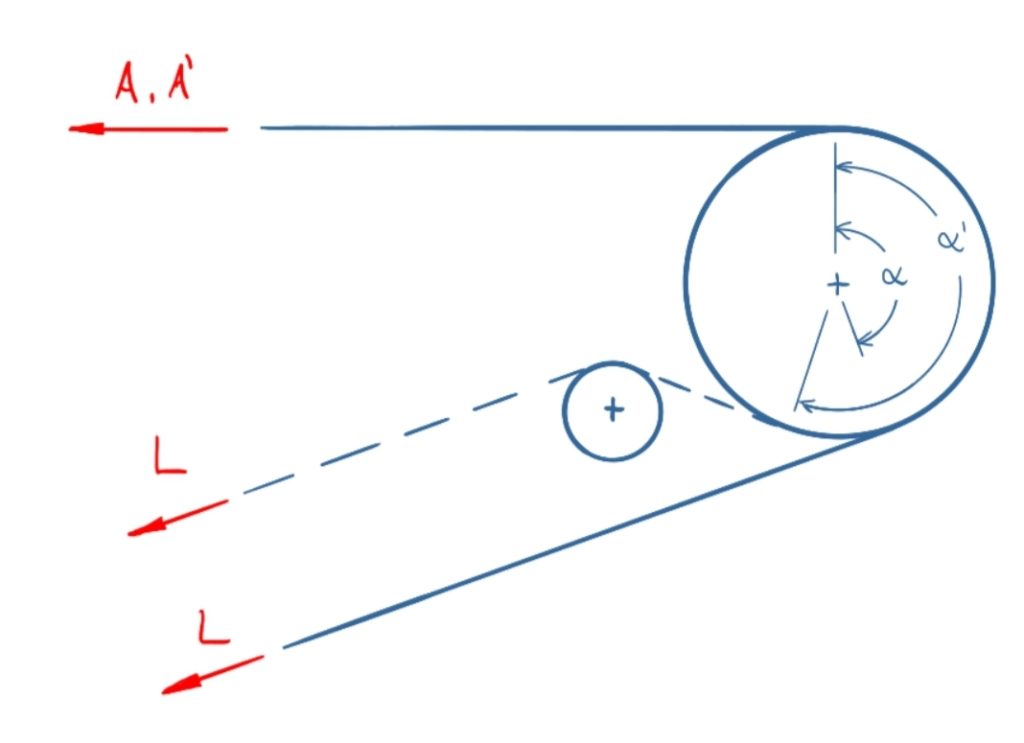
Lösung
Der Zusammenhang zwischen ablaufender und auflaufender Seilkraft wird durch die Seilreibungsformel (Euler-Eytelwein) beschrieben.
\[ \require{cancel} \]Zu a), Größe der Kraft L
\[ \tag{1} A \leq L \cdot e^{µ_0 \cdot \alpha} \]
Die Ungleichung wird im Folgenden vereinfacht zu
\[ \tag{2} L = A \cdot e^{-µ_0 \cdot \alpha} \]
\[ \tag{3} L = 890 N \cdot e^{-0.3 \cdot \frac{8}{9} \cdot \pi} \]
\[ \tag{4} L = 385 N \]
Zu b), Erhöhung der Kraft im Arbeitstrum
Die Berechnung des erforderlichen Umschlingungswinkels für die erhöhte Zugkraft im Lasttrum erfolgt durch folgende Beziehung
\[ \tag{5} L = A' \cdot e^{-µ_0 \cdot \alpha\,'} \]
\[ \tag{6} \frac{A'}{L} = e^{µ_0 \cdot \alpha\,'} \]
\[ \tag{7} \alpha\,' = \frac{\ln \left( \frac{A'}{L} \right)}{µ_0} \]
\[ \tag{8} \alpha\,' = \frac{\ln \left( \frac{1100 N}{385 N} \right)}{0.3} \]
Der notwendige Umschlingungswinkel beträgt damit in Bogenmaß
\[ \tag{9} \alpha\,' = 3,5 rad \]
bzw. in ° umgerechnet
\[ \tag{10} \alpha\,' = 200° \]
Hier gibt es weitere Aufgaben mit Lösungen zum Thema Reibung.
Werbung




