Werbung
Diese Übung zeigt die Lösung für die klassische Mechanik-Übung "Leiter an der Wand" und befasst sich mit den folgenden Fragen:
- Welche Kräfte treten bei einer Leiter an der Wand auf?
- Wann rutscht eine Leiter an der Wand weg?
Unten auf der Seite befindet sich ein Onlinerechner zum Testen verschiedener Kombinationen von Haftreibungskoeffizienten, Längen und Winkeln.
Aufgabe
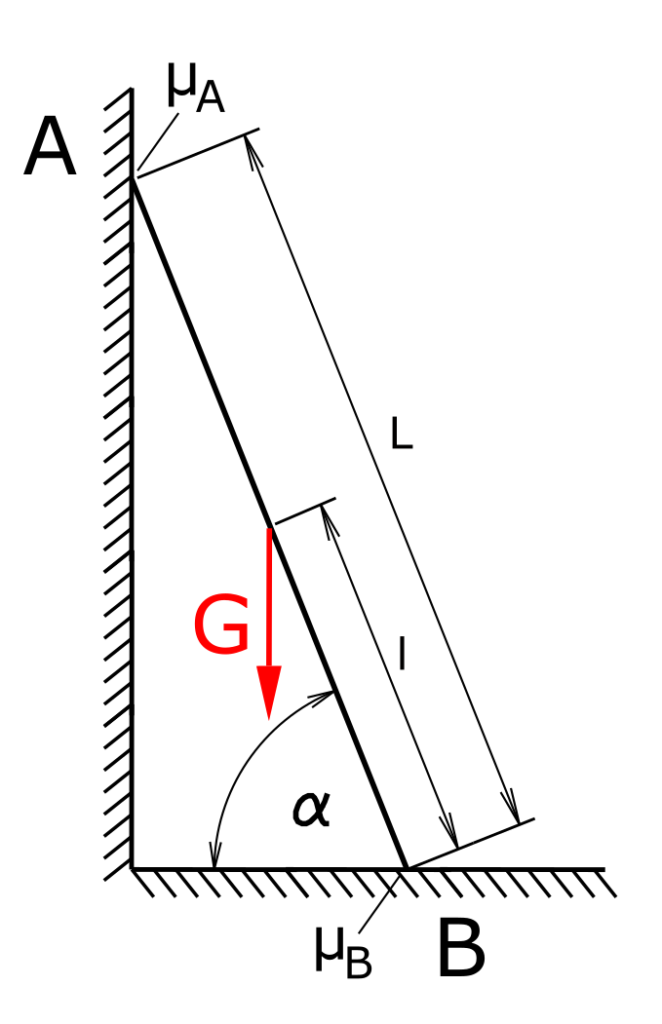
Eine Leiter lehnt an einer Wand. An Boden und Wand liegen unterschiedliche Materialien vor, so dass sich die Haftreibungswerte unterscheiden. Wie weit (Abstand l) kann eine Person mit der Gewichtskraft G auf die Leiter steigen, ohne dass sie wegrutscht?
Lösung
Als Video
Schriftliche Lösung
Zur Lösung der Aufgabe wird die Leiter im ersten Schritt freigeschnitten. Es wird das x-y-Koordinatensystem festgelegt, linksdrehende Momente sind positiv.
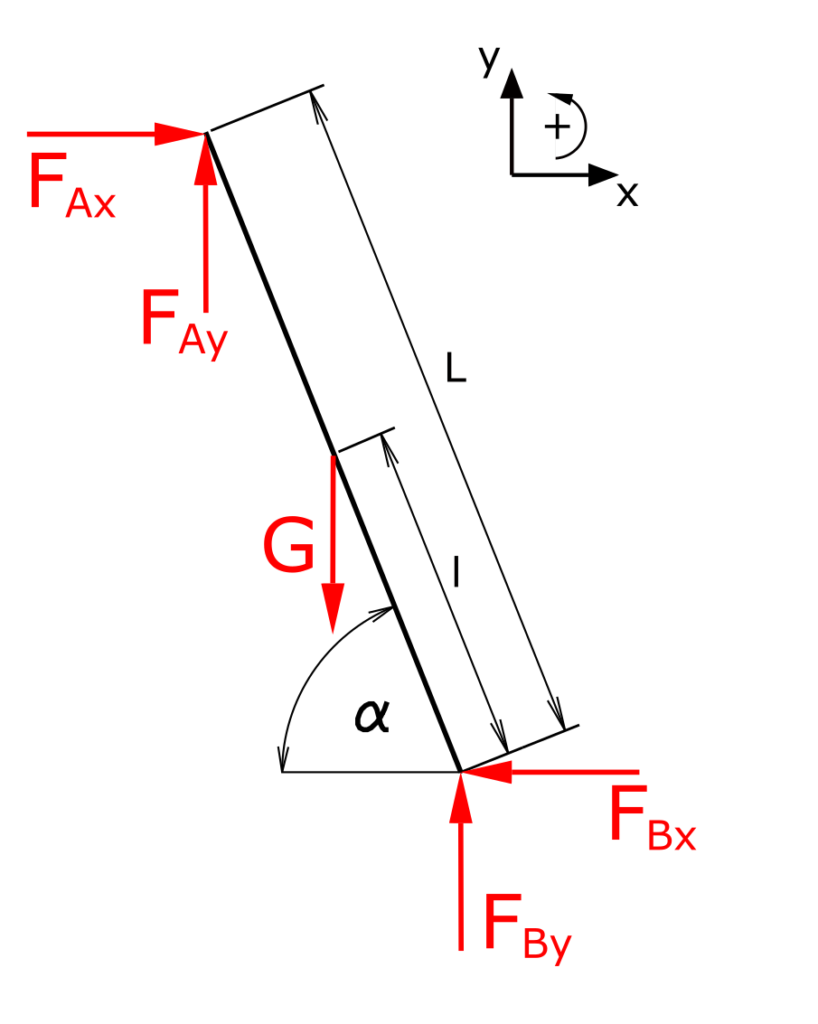
Als nächstes werden die Kräftebilanzen und die Momentenbilanz um B notiert.
\[ \require{cancel} \]Das Kräftegleichgewicht in x-Richtung lautet
\[ \tag{1} \sum F_x = 0 = F_{Ax} - F_{Bx} \]
Das Kräftegleichgewicht in y-Richtung lautet
\[ \tag{2} \sum F_y = 0 = F_{Ay} + F_{By} - G \]
Das Momentengleichgewicht um B ist
\[ \tag{3} \sum M(B) = 0 = G \cdot l \cdot \cos \alpha - F_{Ay} \cdot L \cdot \cos \alpha - F_{Ax} \cdot L \cdot \sin \alpha \]
Die Kräfte FAy und FBx sind jeweils abhängig von ihren Normalkräften und Haftreibungskoeffizienten.
\[ \require{cancel} \]\[ \tag{4} F_{Ay} = F_{Ax} \cdot µ_A \]
\[ \tag{5} F_{Bx} = F_{By} \cdot µ_B \]
Gleichung (1) wird nach FAx aufgelöst und FBx aus Gleichung (5) eingesetzt:
\[ \require{cancel} \]\[ \tag{6} F_{Ax} = F_{By} \cdot µ_B \]
Das gewonnene Ergebnis wird direkt in Gleichung (4) eingesetzt.
\[ \tag{7} F_{Ay} = F_{By} \cdot µ_A \cdot µ_B \]
FAy wird in der Kräftebilanz in y-Richtung, Gleichung (2), eingesetzt und die Gleichung nach FBy aufgelöst:
\[ \require{cancel} \]\[ \tag{8} 0 = F_{By} + F_{By} \cdot µ_A \cdot µ_B - G \]
\[ \tag{9} F_{By} = \frac{G}{µ_A \cdot µ_B + 1} \]
Damit können nun auch unmittelbar FAx und FAy ausgerechnet werden.
\[ \tag{10} F_{Ax} = \frac{G \cdot µ_B}{µ_A \cdot µ_B + 1} \]
\[ \tag{11} F_{Ay} = \frac{G \cdot µ_A \cdot µ_B}{µ_A \cdot µ_B + 1} \]
Die Momentenbilanz (3) wird umgestellt nach der Länge l und die berechneten Größen eingesetzt.
\[ \require{cancel} \]\[ \tag{12} l=\frac{{F_{\mathit{Ax}}} \cdot L \cdot \sin{\left( \alpha \right) }+{F_{\mathit{Ay}}} \cdot L \cdot \cos{\left( \alpha \right) }}{G \cdot \cos{\left( \alpha \right) }} \]
\[ \tag{13} l=\frac{\frac{G \cdot L \cdot {µ_B} \cdot \sin{\left( \alpha \right) }}{{µ_A} \cdot {µ_B}+1}+\frac{G \cdot L \cdot {µ_A} \cdot {µ_B} \cdot \cos{\left( \alpha \right) }}{{µ_A} \cdot {µ_B}+1}}{G \cdot \cos{\left( \alpha \right) }}\]
bzw. gekürzt und umgeformt:
\[ \tag{14} l=\frac{L \cdot {µ_B} \cdot \sin{\left( \alpha \right) }+L \cdot {µ_A} \cdot {µ_B} \cdot \cos{\left( \alpha \right) }}{\left( {µ_A} \cdot {µ_B}+1\right) \cdot \cos{\left( \alpha \right) }}\]
Die gesuchte Länge ist damit ermittelt. Erwartungsgemäß konnte die Gewichtskraft zur Berechnung herausgekürzt werden, sie hat also keinen Einfluss auf das Ergebnis.
Onlinerechner
Das vorab ermittelte Ergebnis kann hier getestet werden.
Wenn man die Werte eingibt, wird man feststellen, dass die Funktion bereits für einen Winkel von 0° (oder wenn man das Feld leer lässt) oder sehr kleine Winkel eine Länge berechnet.
Was bedeutet das?
Das erscheint auf den ersten Blick vielleicht falsch, ist aber korrekt. Die berechnete Länge liegt bis zu einem bestimmten Winkel unterhalb des Schwerpunkts der Leiter. Jegliche Gewichtskraft, die oberhalb dieser Länge auf die Leiter wirkt, würde ein Wegrutschen der Leiter bewirken. Und das ist, durch den in der Mitte der Leiter liegenden Schwerpunkt, bis zu einem bestimmten Winkel der Fall. Als Beispiel: eine Leiter mit Haftreibungskoeffizienten von 0,5 sowohl in A und B würde erst ab einem Winkel von ca. 37° alleine stehen bleiben.
Und jetzt viel Spaß beim Ausprobieren:
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Reibung.
Werbung




