This exercise shows the solution for the classical mechanics exercise "ladder on a wall" and addresses the following questions:
- Which forces occur on a ladder leaning against a wall?
- When does the ladder slip?
At the bottom of the page is an online calculator for testing various combinations of coefficients of static friction, lengths and angles.
Task
A ladder is leaning against a wall. There are different materials on the floor and wall, so that the static friction values differ. How high (distance l) can a person with the weight G climb the ladder without slipping?
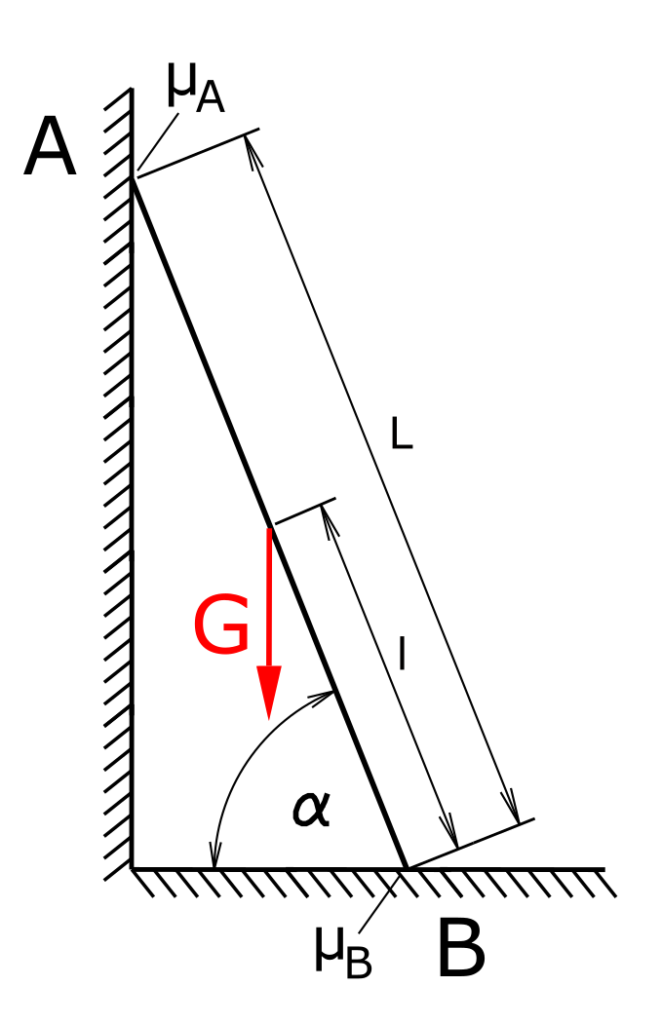
Solution
To solve the task, the ladder is cut free in the first step. The coordinate system is set to x-y and left turning moments are positive.
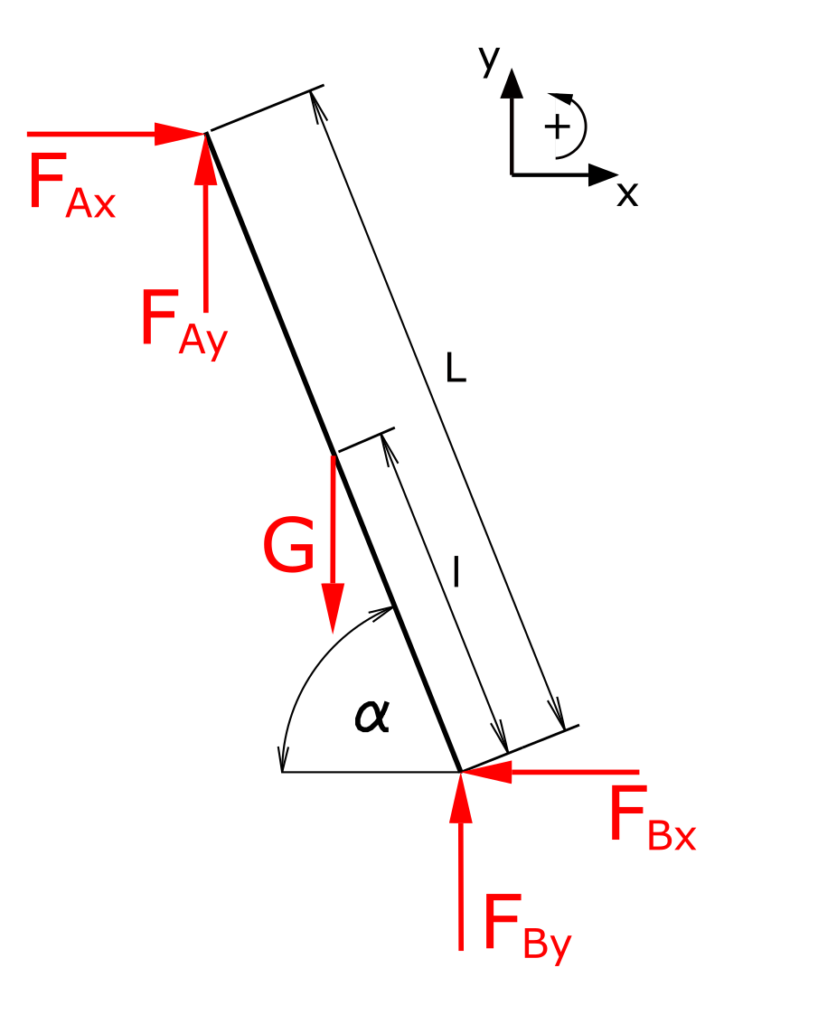
Next, the balance of forces in x- and y-direction and the balance of moments around B are noted.
\[ \require{cancel} \]The balance of forces in x-direction is
\[ \tag{1} \sum F_x = 0 = F_{Ax} - F_{Bx} \]
The balance of forces in y-direction is
\[ \tag{2} \sum F_y = 0 = F_{Ay} + F_{By} - G \]
The balance of moments around B is
\[ \tag{3} \sum M(B) = 0 = G \cdot l \cdot \cos \alpha - F_{Ay} \cdot L \cdot \cos \alpha - F_{Ax} \cdot L \cdot \sin \alpha \]
The forces FAy and FBx are each dependent on their normal forces and coefficients of static friction.
\[ \require{cancel} \]\[ \tag{4} F_{Ay} = F_{Ax} \cdot µ_A \]
\[ \tag{5} F_{Bx} = F_{By} \cdot µ_B \]
Equation (1) is solved for FAx and FBx from equation (5) is inserted:
\[ \require{cancel} \]\[ \tag{6} F_{Ax} = F_{By} \cdot µ_B \]
The result obtained is inserted directly into equation (4).
\[ \tag{7} F_{Ay} = F_{By} \cdot µ_A \cdot µ_B \]
FAy is used in the balance of forces in the y-direction, equation (2), and the equation is solved for FBy:
\[ \require{cancel} \]\[ \tag{8} 0 = F_{By} + F_{By} \cdot µ_A \cdot µ_B - G \]
\[ \tag{9} F_{By} = \frac{G}{µ_A \cdot µ_B + 1} \]
This means that FAx and FAy can now also be calculated.
\[ \tag{10} F_{Ax} = \frac{G \cdot µ_A}{µ_A \cdot µ_B + 1} \]
\[ \tag{11} F_{Ay} = \frac{G \cdot µ_A \cdot µ_B}{µ_A \cdot µ_B + 1} \]
The moment balance (3) is converted according to the length l and the calculated values are used.
\[ \require{cancel} \]\[ \tag{12} l=\frac{{F_{\mathit{Ax}}} \cdot L \cdot \sin{\left( \alpha \right) }+{F_{\mathit{Ay}}} \cdot L \cdot \cos{\left( \alpha \right) }}{G \cdot \cos{\left( \alpha \right) }} \]
\[ \tag{13} l=\frac{\frac{G \cdot L \cdot {µ_B} \cdot \sin{\left( \alpha \right) }}{{µ_A} \cdot {µ_B}+1}+\frac{G \cdot L \cdot {µ_A} \cdot {µ_B} \cdot \cos{\left( \alpha \right) }}{{µ_A} \cdot {µ_B}+1}}{G \cdot \cos{\left( \alpha \right) }}\]
or shortened and reshaped:
\[ \tag{14} l=\frac{L \cdot {µ_B} \cdot \sin{\left( \alpha \right) }+L \cdot {µ_A} \cdot {µ_B} \cdot \cos{\left( \alpha \right) }}{\left( {µ_A} \cdot {µ_B}+1\right) \cdot \cos{\left( \alpha \right) }}\]
The length you are looking for is now determined. As expected, the weight force could be reduced for the calculation, so it has no influence on the result.
Online calculator
The result can be tested here.
If you enter the values, you will find that the function calculates a length for an angle of 0° (or if you leave the field empty) or fot very small angles.
What does this mean?
This may seem wrong at first glance, but it is correct. The calculated length is below the center of gravity of the ladder up to a certain angle. Any weight acting on the ladder above this length would cause the ladder to slip away. And because of the center of gravity in the middle of the ladder, this is the case up to a certain angle. As an example: a ladder with a coefficient of static friction of 0.5 in both A and B would only stand alone at an angle of approx. 37°.
And now try it for yourself:
We have a lot more interesting exercises regarding statics here.

