Werbung
Diese Übung befasst sich mit einer Bremse mit doppelt wirkendem Hebel und behandelt folgende Fragen:
- Wie bestimmt man das Bremsmoment für eine Bandbremse?
- Wie wendet man die Seilreibungsformel an?
- Gibt es Bandbremsen, die in beiden Drehrichtungen das gleiche Bremsmoment erzeugen?
Eine Übersicht mit Haft- und Gleitreibungswerten gibt es hier.
Aufgabe
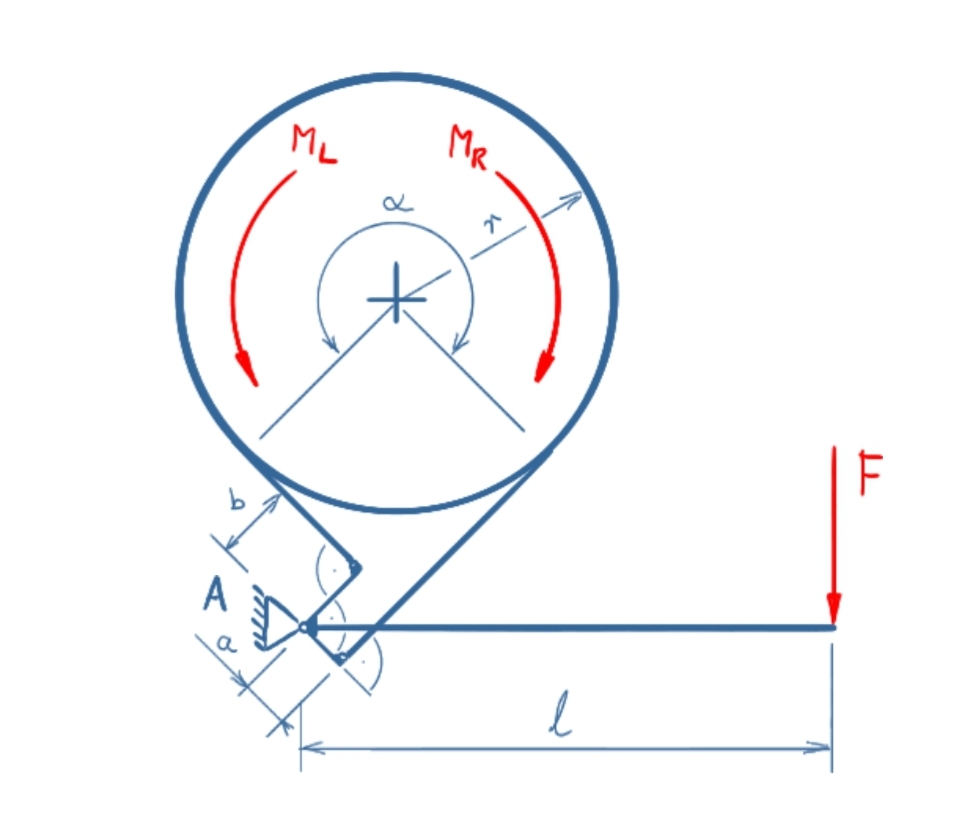
Eine Bremse mit doppelt wirkendem Hebel wird mit der Kraft F betätigt. Zu bestimmen sind die maximalen Bremsmomente im Rechtslauf und im Linkslauf.
Lösung
Die Bandbremse wird in zwei Bereiche eingeteilt: den Betätigungshebel und die Trommel mit dem Band. Die Momentengleichgewichte an der Trommel werden für Rechts- und Linkslauf separat betrachtet.
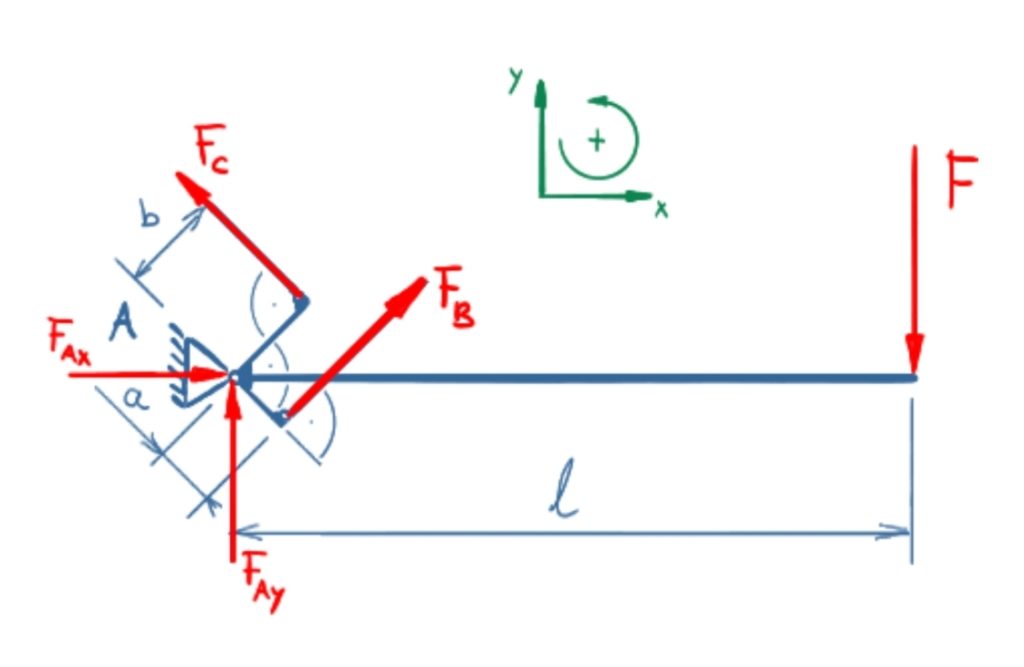
Momente am Betätigungshebel
\[ \tag{1} \sum M(A) = 0 = F_C \cdot b + F_B \cdot a - F \cdot l \]
Linkslauf
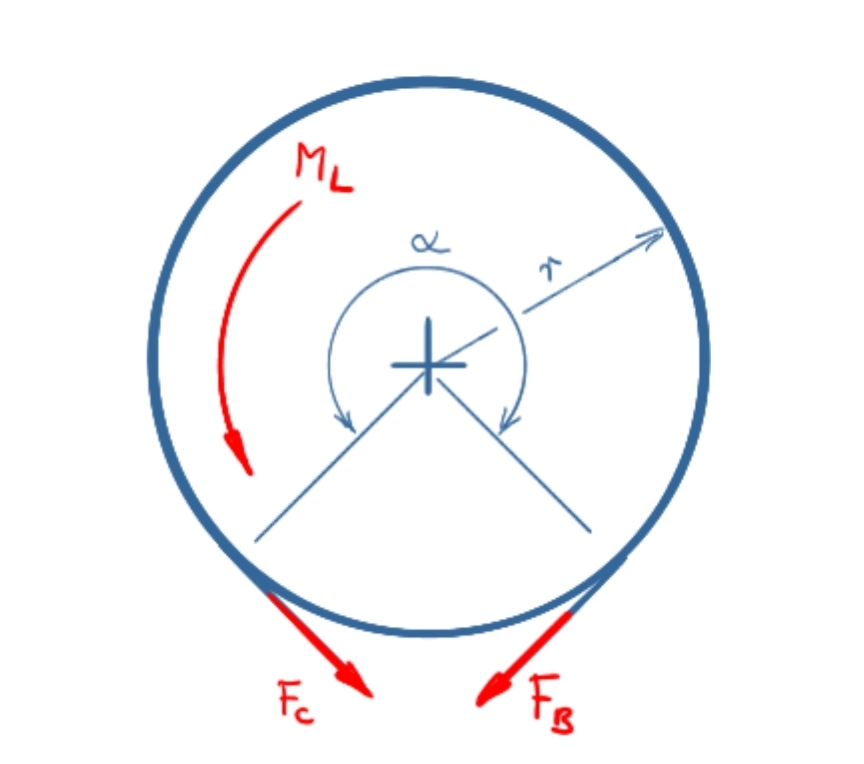
Momente an der Bremstrommel
\[ \tag{2} \sum M = 0 = F_C \cdot r - F_B \cdot r + M_L \]
Die Seilreibungsformel (Euler-Eytelwein) liefert den Zusammenhang zwischen ablaufender und auflaufender Seilkraft:
\[ \tag{3} F_B \leq F_C \cdot e^{µ \cdot \alpha} \]
FB eingesetzt in Gleichung (1) ergibt
\[ \tag{4} 0 = F_C \cdot b + F_C \cdot e^{µ \cdot \alpha} \cdot a - F \cdot l \]
\[ \tag{5} F_C \cdot b + F_C \cdot e^{µ \cdot \alpha} \cdot a = F \cdot l \]
\[ \tag{6} F_C = \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \]
FB und FC können nun in Gleichung (2) eingesetzt werden
\[ \tag{7} 0 = \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot r - \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot e^{µ \cdot \alpha} \cdot r + M_L \]
\[ \tag{8} M_L = \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot e^{µ \cdot \alpha} \cdot r - \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot r \]
\[ \tag{9} M_L = \frac{F \cdot l \cdot r}{b + e^{µ \cdot \alpha} \cdot a} \cdot \left(e^{µ \cdot \alpha} - 1 \right) \]
Damit ist das Bremsmoment für den Linkslauf der Bandbremse bestimmt.
Rechtslauf
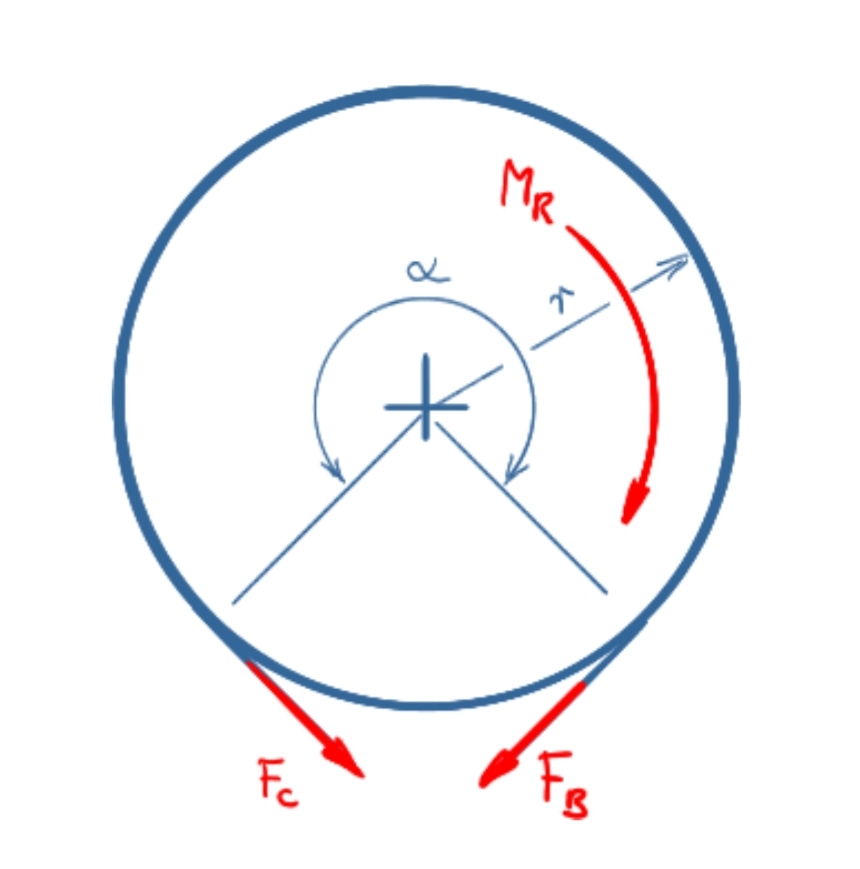
Momente an der Bremstrommel
\[ \tag{10} \sum M = 0 = F_C \cdot r - F_B \cdot r - M_R \]
Die Seilreibungsformel lautet für diesen Fall:
\[ \tag{11} F_C \leq F_B \cdot e^{µ \cdot \alpha} \]
\[ \tag{12} F_B = F_C \cdot e^{-µ \cdot \alpha} \]
FB eingesetzt in Gleichung (1) ergibt
\[ \tag{13} 0 = F_C \cdot b + F_C \cdot e^{-µ \cdot \alpha} \cdot a - F \cdot l \]
\[ \tag{14} F_C = \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \]
FB und FC können nun in Gleichung (10) eingesetzt werden
\[ \tag{15} 0 = \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot r - \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot e^{-µ \cdot \alpha} \cdot r - M_R \]
\[ \tag{16} M_R = \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot r - \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot e^{-µ \cdot \alpha} \cdot r \]
\[ \tag{17} M_R = \frac{F \cdot l \cdot r}{b + e^{-µ \cdot \alpha}\cdot a} \cdot \left( 1 - e^{-µ \cdot \alpha} \right) \]
Damit ist auch das rechtsdrehende Bremsmoment bestimmt.
Es zeigt sich, dass die Bremse mit doppelt wirkendem Hebel eine geschickte Konstruktion ist: Für diese Bremse gilt, wenn die Längen a und b gleich groß sind, wird in beiden Drehrichtungen das gleiche Bremsmoment bzw. Haltemoment erreicht.
Hier gibt es weitere interessante Übungen und Lösungen zum Thema Reibung. Eine Herleitung der Seilreibungsformel kann man an dieser Stelle nachlesen.
Werbung




