Werbung
In dieser Übung wird eine unsymmetrische Last an zwei Seilen betrachtet und folgende Fragen behandelt:
- Wie formuliert man Zwangsbedingungen in Gleichungen?
- Wie stellt man ein Kräftegleichgewicht auf?
- Wie berechnet man einen Winkel mit dem Arkustangens?
Aufgabe
Eine Last mit der Eigengewichtskraft G = 100 N soll an zwei Seilen 1 und 2 so aufgehängt werden, dass die Maße a = 2 m und h = 2 m eingehalten werden und die Kraft in Seil 1 den Wert S1= 80 N annimmt. Wie groß ist l?
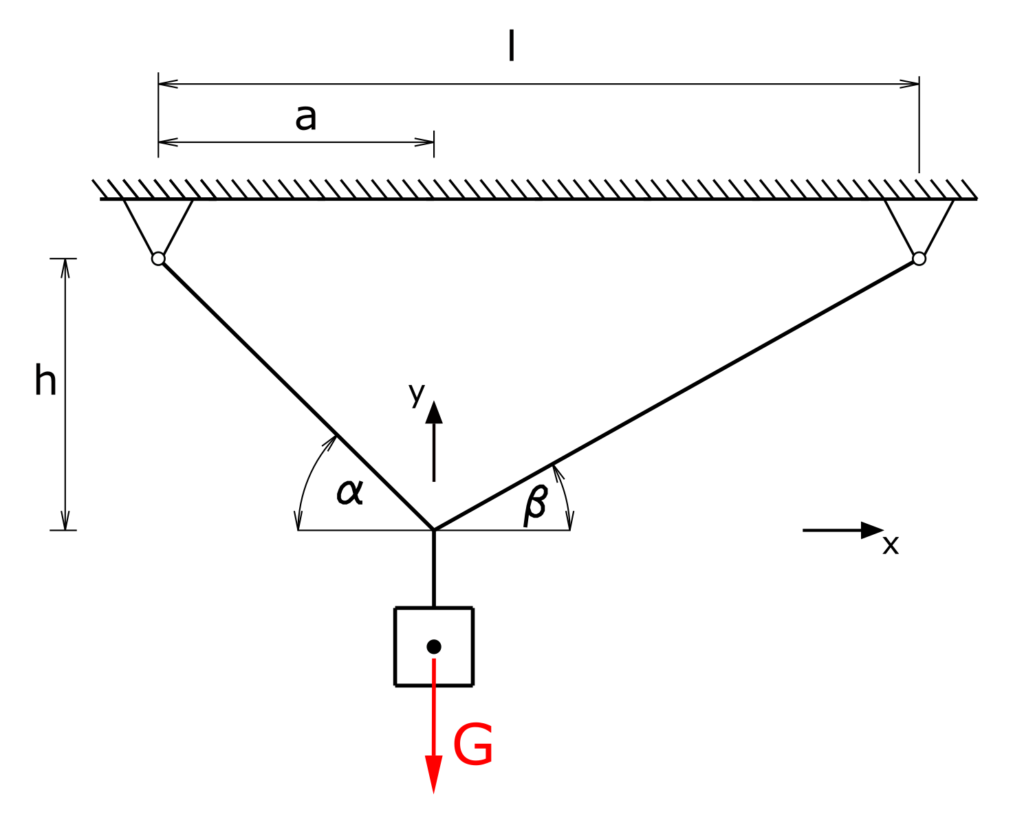
Lösung
Die Kraft G verteilt sich auf die beiden Seilkräfte S1 und S2.
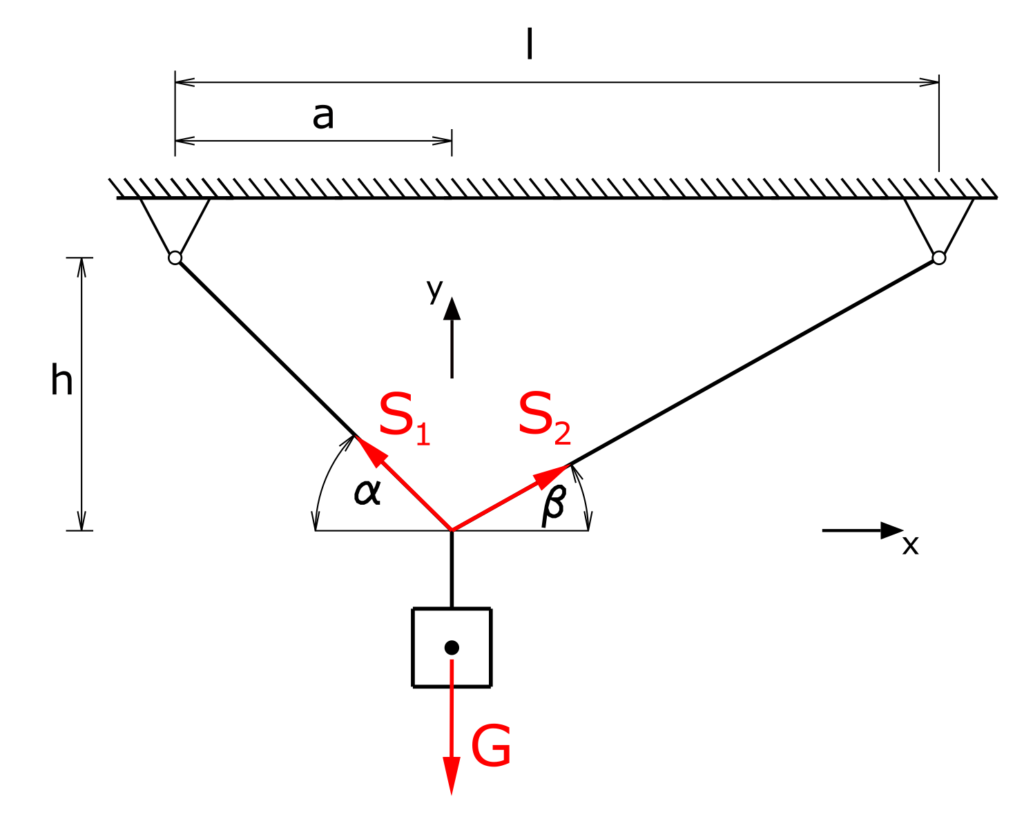
Am Verbindungspunkt der Seile entsteht ein zentrales ebenes Kräftesystem, alle Kräfte haben einen gemeinsamen Angriffspunkt. Die Seilkräfte können in ihre jeweiligen Komponenten in x- und y-Richtung zerlegt werden. (Die beiden Kräfte S1y und S2y sind der Übersichtlichkeit halber nebeneinander eingezeichnet, greifen aber auch in dem gemeinsamen Punkt an.)
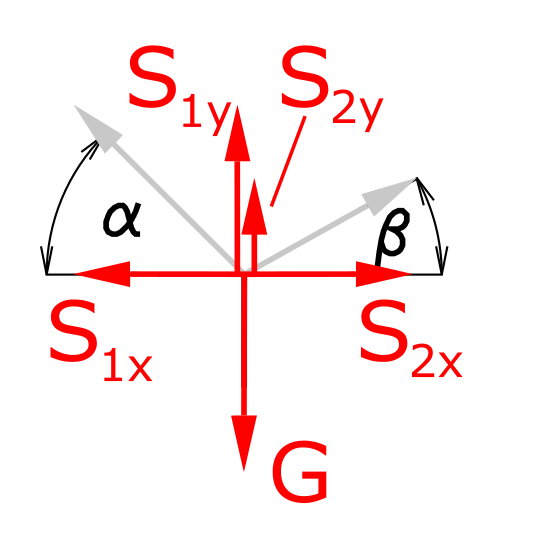
Es werden die Kräftegleichgewichte für die x- und y-Richtung aufgestellt. Hierzu werden die Seilkräfte in ihre jeweiligen Komponenten zerlegt.
\[\tag{1} \sum F_x = 0 = -S_{1x} + S_{2x} \]
\[\tag{2} \sum F_y = 0 = S_{1y} + S_{2y} - G \]
Der Winkel α lässt sich aus den gegebenen Längen h und a berechnen.
\[\tag{3} \alpha = arctan \left( \frac{h}{a} \right) = 45° \]
Mit diesem Winkel und der vorgegebenen Kraft für Seil 1 kann die x-Komponenten der Kraft in Seil 1 berechnet werden.
\[\tag{4} S_{1x} = S_1 cos \alpha \]
\[\tag{5} S_{1x} = 80 N \cdot cos 45° = 56.6 N \]
\[\tag{6} S_{2x} = S_{1x} = 56.6 N \]
Und ebenso die y-Komponente.
\[\tag{7} S_{1y} = S_1 sin \alpha \]
\[\tag{8} S_{1y} = 80 N \cdot sin 45° = 56.6 N \]
Aus Gleichung 2 ergibt sich
\[\tag{9} S_{2y} = G - S_{1y} \]
\[\tag{10} S_{2y} = 100 N - 56.6 N = 43.4 N \]
Die Kraft in Seil 2 wird mit dem Satz des Pythagoras berechnet.
\[\tag{11} S_2 = \sqrt{S_{2x}^2 + S_{2y}^2} \]
\[\tag{12} S_2 = \sqrt{56.6^2 N^2 + 43.4^2 N^2} = 71.3 N \]
Der Winkel β ergibt sich aus
\[\tag{13} S_{2x} = S_2 cos \beta \]
\[\tag{14} \beta = arccos \left( \frac{S_{2x}}{S_2} \right) = 37.5° \]
Der Winkel β steht im Zusammenhang mit h, l und a. Hieraus kann nun die geforderte Länge l berechnet werden.
\[\tag{15} \beta = arctan \left( \frac{h}{l-a} \right) \]
\[\tag{16} tan \beta = \frac{h}{l-a} \]
\[\tag{17} l = \frac{h}{tan \beta} + a = 4.6 m \]
Damit ist der notwendige Abstand der beiden Aufhängungspunkte für die unsymmetrische Last an zwei Seilen bestimmt. Hier gibt es eine ähnliche Aufgabe mit einer symmetrischen Aufhängung einer Last.
Werbung




