Werbung
In dieser Übung wird die Biegelinie für einen Träger mit teilweiser Streckenlast, Einzelkraft und Moment berechnet.
Aufgabe
Ein durchgehender Träger auf einem Festlager und einem Loslager wird auf der Länge l durch die Streckenlast q belastet, zusätzlich wirkt die Kraft F und am Loslager das Moment M. Es ist die Biegelinie des Trägers zu bestimmen.
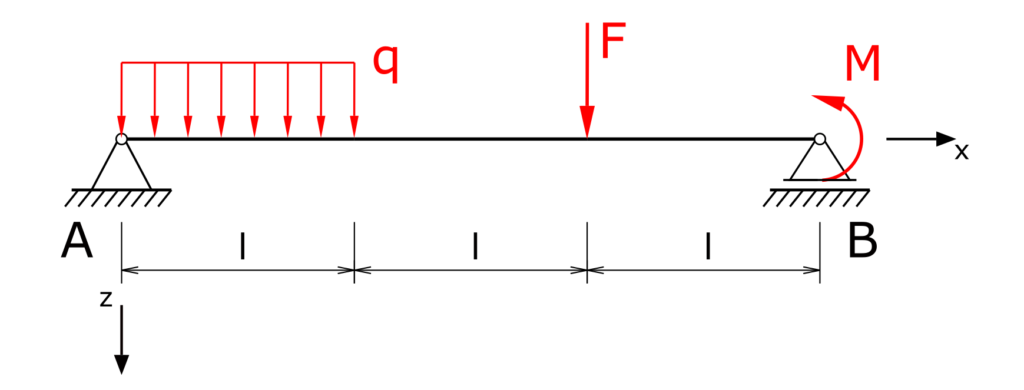
Lösung
Im ersten Schritt werden die Gleichungen für die Lagerreaktionen ermittelt. Für die Ermittlung der Schnittgrößen wird der Träger in drei Bereiche eingeteilt. In den nachfolgenden Gleichungen werden die Horizontalkräfte nicht weiter betrachtet, da sie offensichtlich Null sind. Linksdrehende Momente sind positiv.
Ermittlung der Lagerreaktionen
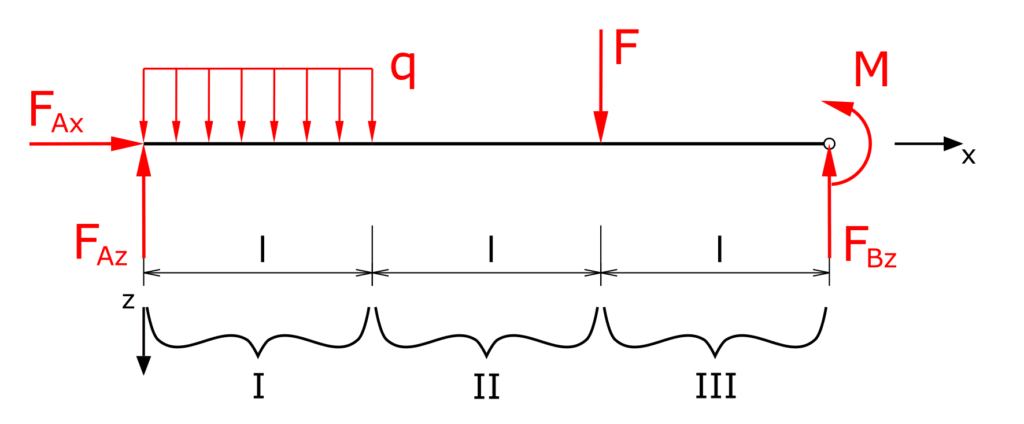
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{1} \sum F_z = 0 = -F_{Az} - F_{Bz} + F + \int_0^{l}{qdx} \]
\[ \tag{2} 0 = -F_{Az} - F_{Bz} + F + q \cdot l \]
Die Summe der der Momente um A
\[ \tag{3} \sum M(A) = 0 = 3 \cdot F_{Bz} \cdot l - 2 \cdot F \cdot l - \int_0^{l}{qxdx} + M \]
\[ \tag{4} 0 = 3 \cdot F_{Bz} \cdot l - 2 \cdot F \cdot l - \frac{1}{2} q \cdot l^2 + M \]
Die beiden Lagerreaktionskräfte FAz und FBz können nun durch Umstellung der Gleichungen berechnet werden. Sie betragen:
\[ \tag{5} {F_{\mathit{Bz}}}=\frac{{{l}^{2}} q+4 F l-2 M}{6 l} \]
\[ \tag{6} {F_{\mathit{Az}}}=\frac{5 {{l}^{2}} q+2 F l+2 M}{6 l}\]
Als nächster Schritt werden die Schnittgrößen in den Bereichen I bis III ermittelt. Um die Funktion der Streckenlast von 0 bis x integrieren zu können, wird sie als Funktion der Hilfskoordinate ξ formuliert. Normalkräfte werden mit N bezeichnet, Querkräfte mit Q und Biegemomente mit Mb.
Ermittlung der Schnittgrößen
Bereich I
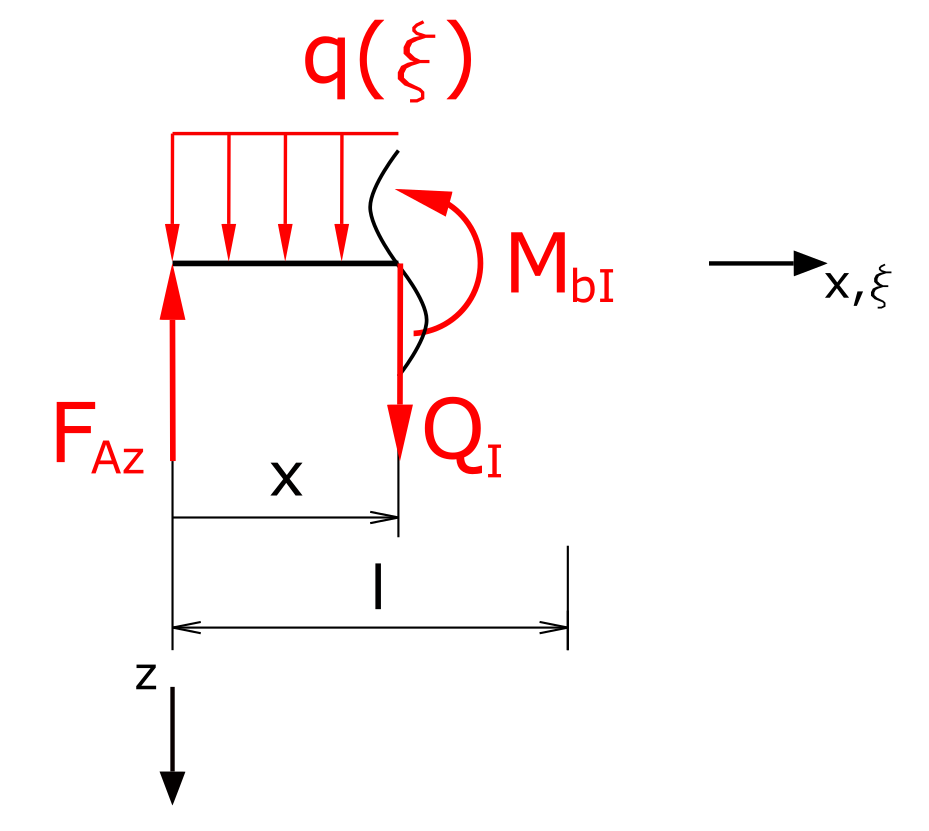
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{7} \sum F_z = 0 = Q_I - F_{Az} + \int_0^{x}{qd\xi} \]
\[ \tag{8} {Q_I}=-\frac{6 l q x-5 {{l}^{2}} q-2 F l-2 M}{6 l} \]
Die Summe der der Momente um x
\[ \tag{9} \sum M(x) = 0 = \int_0^{x}{q (x-\xi) d \xi} - F_{Az} \cdot x + M_{bI} \]
\[ \tag{10} {M_{\mathit{bI}}}=-\frac{3 l q\, {{x}^{2}}+\left( -5 {{l}^{2}} q-2 F l-2 M\right) x}{6 l}\]
Bereich II
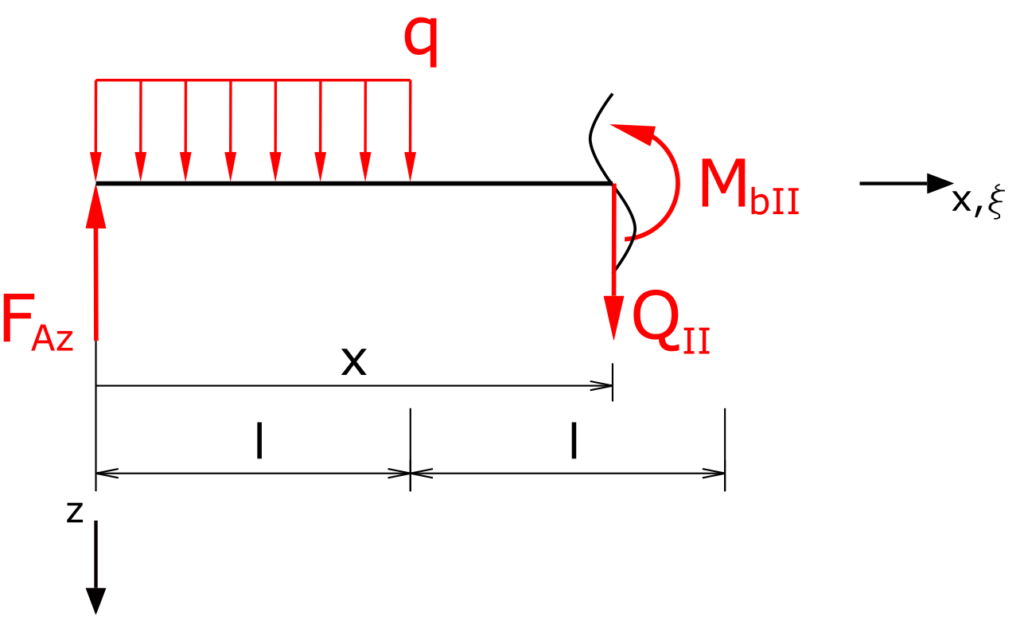
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{11} \sum F_z = 0 = Q_{II} - F_{Az} + \int_0^{l}{q d \xi} \]
\[ \tag{12} {Q_{\mathit{II}}}=-\frac{{{l}^{2}} q-2 F l-2 M}{6 l}\]
Die Summe der der Momente um x
\[ \tag{13} \sum M(x) = 0 = \int_0^{l}{q (x - \xi) d \xi} - F_{Az} \cdot x + M_{bII} \]
\[ \tag{14} {M_{\mathit{bII}}}=-\frac{\left( {{l}^{2}} q-2 F l-2 M\right) x-3 {{l}^{3}} q}{6 l}\]
Bereich III
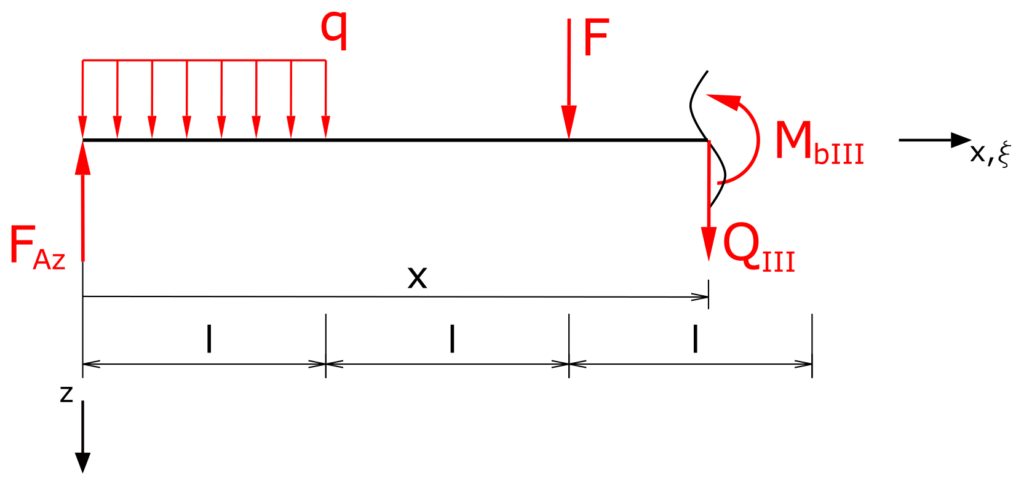
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{15} \sum F_z = 0 = Q_{III} - F_{Az} + F + \int_0^{l}{q d \xi} \]
\[ \tag{16} {Q_{\mathit{III}}}=-\frac{{{l}^{2}} q+4 F l-2 M}{6 l}\]
Die Summe der der Momente um x
\[ \tag{17} \sum M(x) = 0 = \int_0^{l}{q (x - \xi) d \xi} - F_{Az} \cdot x + F \cdot (x - 2 \cdot l) + M_{bIII} \]
\[ \tag{18} {M_{\mathit{bIII}}}=-\frac{\left( {{l}^{2}} q+4 F l-2 M\right) x-3 {{l}^{3}} q-12 F\, {{l}^{2}}}{6 l}\]
Als nächstes werden die Funktionen der Biegelinien berechnet.
Biegelinien
Die Funktion der Biegelinie wird als w bezeichnet, bzw. die erste Ableitung als w' und die zweite Ableitung als w''. Der Elastizitätsmodul ist E und das Flächenträgheitsmoment I.
Bereich I
\[ \tag{19} {M_{\mathit{bI}}}=-\frac{3 l q\, {{x}^{2}}+\left( -5 {{l}^{2}} q-2 F l-2 M\right) x}{6 l} \]
\[ \tag{20} w''_I = - \frac{1}{E \cdot I} M_{bI} \]
\[ \tag{21} w''_I = -\frac{-3 l q\, {{x}^{2}}-\left( -5 {{l}^{2}} q-2 F l-2 M\right) x}{6 E I l}\]
\[ \tag{22} w'_I = {c_1}-\frac{\frac{\left( 5 {{l}^{2}} q+2 F l+2 M\right) \, {{x}^{2}}}{2}-l q\, {{x}^{3}}}{6 E I l}\]
\[ \tag{23} w_I = -\frac{\frac{\left( 5 {{l}^{2}} q+2 F l+2 M\right) \, {{x}^{3}}}{6}-\frac{l q\, {{x}^{4}}}{4}}{6 E I l}+{c_1} x+{c_2}\]
Bereich II
\[ \tag{24} {M_{\mathit{bII}}}=-\frac{\left( {{l}^{2}} q-2 F l-2 M\right) x-3 {{l}^{3}} q}{6 l}\]
\[ \tag{25} w''_{II} = - \frac{1}{E \cdot I} M_{bII} \]
\[ \tag{26} w''_{II} = -\frac{3 {{l}^{3}} q-\left( {{l}^{2}} q-2 F l-2 M\right) x}{6 E I l}\]
\[ \tag{27} w'_{II} = {c_3}-\frac{\frac{\left( -{{l}^{2}} q+2 F l+2 M\right) \, {{x}^{2}}}{2}+3 {{l}^{3}} q x}{6 E I l} \]
\[ \tag{28} w_{II} = -\frac{\frac{\left( -{{l}^{2}} q+2 F l+2 M\right) \, {{x}^{3}}}{6}+\frac{3 {{l}^{3}} q\, {{x}^{2}}}{2}}{6 E I l}+{c_3} x+{c_4}\]
Bereich III
\[ \tag{29} {M_{\mathit{bIII}}}= -\frac{\left( {{l}^{2}} q+4 F l-2 M\right) x-3 {{l}^{3}} q-12 F\, {{l}^{2}}}{6 l}\]
\[ \tag{30} w''_{III} = - \frac{1}{E \cdot I} M_{bIII} \]
\[ \tag{31} w''_{III} = -\frac{-\left( {{l}^{2}} q+4 F l-2 M\right) x+3 {{l}^{3}} q+12 F\, {{l}^{2}}}{6 E I l}\]
\[ \tag{32} w'_{III} = {c_5}-\frac{\frac{\left( -{{l}^{2}} q-4 F l+2 M\right) \, {{x}^{2}}}{2}+3 {{l}^{3}} q x+12 F\, {{l}^{2}} x}{6 E I l}\]
\[ \tag{33} w_{III} = -\frac{\frac{\left( -{{l}^{2}} q-4 F l+2 M\right) \, {{x}^{3}}}{6}+\frac{3 {{l}^{3}} q\, {{x}^{2}}}{2}+6 F\, {{l}^{2}}\, {{x}^{2}}}{6 E I l}+{c_5} x+{c_6}\]
Die Integrationskonstanten werden über die Rand- und Nebenbedingungen ermittelt.
Rand- und Nebenbedingungen
Die Durchbiegung an der Stelle x = 0 ist gleich Null.
\[ \tag{34} w_I(x=0)=0=\mathit{c_2} \]
Die Durchbiegung an der Stelle x = l ist für Biegelinie I und Biegelinie II gleich groß.
\[ \tag{35} w_I(x=l)=w_{II}(x=l) \]
\[ \tag{36} -\frac{\frac{{{l}^{3}}\, \left( 5 {{l}^{2}} q+2 F l+2 M\right) }{6}-\frac{{{l}^{5}} q}{4}}{6 E I l}+{c_1} l+{c_2}=-\frac{\frac{{{l}^{3}}\, \left( -{{l}^{2}} q+2 F l+2 M\right) }{6}+\frac{3 {{l}^{5}} q}{2}}{6 E I l}+{c_3} l+{c_4} \]
Die Neigung an der Stelle x = l ist für Biegelinie I und Biegelinie II gleich groß.
\[ \tag{37} w'_I(x=l)=w'_{II}(x=l) \]
\[ \tag{38} {c_1}-\frac{\frac{{{l}^{2}}\, \left( 5 {{l}^{2}} q+2 F l+2 M\right) }{2}-{{l}^{4}} q}{6 E I l}={c_3}-\frac{\frac{{{l}^{2}}\, \left( -{{l}^{2}} q+2 F l+2 M\right) }{2}+3 {{l}^{4}} q}{6 E I l} \]
Die Durchbiegung an der Stelle x = 2l ist für Biegelinie II und Biegelinie III gleich groß.
\[ \tag{39} w_{II}(x=2l)=w_{III}(x=2l) \]
\[ -\frac{\frac{4 {{l}^{3}}\, \left( -{{l}^{2}} q+2 F l+2 M\right) }{3}+6 {{l}^{5}} q}{6 E I l}+2 {c_3} l+{c_4}=... \]
\[ \tag{40} ...=-\frac{\frac{4 {{l}^{3}}\, \left( -{{l}^{2}} q-4 F l+2 M\right) }{3}+6 {{l}^{5}} q+24 F\, {{l}^{4}}}{6 E I l}+2 {c_5} l+{c_6} \]
Die Neigung an der Stelle x = 2l ist für Biegelinie II und Biegelinie III gleich groß.
\[ \tag{41} w'_{II}(x=2l)=w'_{III}(x=2l) \]
\[ {c_3}-\frac{2 {{l}^{2}}\, \left( -{{l}^{2}} q+2 F l+2 M\right) +6 {{l}^{4}} q}{6 E I l}=... \]
\[ \tag{42} ...={c_5}-\frac{2 {{l}^{2}}\, \left( -{{l}^{2}} q-4 F l+2 M\right) +6 {{l}^{4}} q+24 F\, {{l}^{3}}}{6 E I l} \]
Die Durchbiegung an der Stelle x = 3l ist gleich Null.
\[ \tag{43} w_{III}(x=3l)=0 \]
\[ \tag{44} 0 = -\frac{\frac{9 {{l}^{3}}\, \left( -{{l}^{2}} q-4 F l+2 M\right) }{2}+\frac{27 {{l}^{5}} q}{2}+54 F\, {{l}^{4}}}{6 E I l}+3 {c_5} l+{c_6} \]
Die Unbekannten können nun aufgelöst werden. Sie ergeben sich zu
\[ \tag{45} {c_1}=\frac{25 {{l}^{3}} q+32 F\, {{l}^{2}}+36 M l}{72 E I}\]
\[ \tag{46} {c_2}=0\]
\[ \tag{47} {c_3}=\frac{37 {{l}^{3}} q+32 F\, {{l}^{2}}+36 M l}{72 E I}\]
\[ \tag{48} {c_4}=-\frac{{{l}^{4}} q}{24 E I}\]
\[ \tag{49} {c_5}=\frac{37 {{l}^{3}} q+176 F\, {{l}^{2}}+36 M l}{72 E I}\]
\[ \tag{50} {c_6}=-\frac{{{l}^{4}} q+32 F\, {{l}^{3}}}{24 E I}\]
Abschließend können die drei Funktionen der Biegelinien nun wie folgt beschrieben werden:
\[ \tag{51} w_I(x) = \frac{\left( 25 {{l}^{3}} q+32 F\, {{l}^{2}}+36 M l\right) x}{72 E I}-\frac{\frac{\left( 5 {{l}^{2}} q+2 F l+2 M\right) \, {{x}^{3}}}{6}-\frac{l q\, {{x}^{4}}}{4}}{6 E I l}\]
\[ \tag{52} w_{II}(x) = -\frac{\frac{\left( -{{l}^{2}} q+2 F l+2 M\right) \, {{x}^{3}}}{6}+\frac{3 {{l}^{3}} q\, {{x}^{2}}}{2}}{6 E I l}+\frac{\left( 37 {{l}^{3}} q+32 F\, {{l}^{2}}+36 M l\right) x}{72 E I}-\frac{{{l}^{4}} q}{24 E I}\]
\[ w_{III}(x) = -\frac{\frac{\left( -{{l}^{2}} q-4 F l+2 M\right) \, {{x}^{3}}}{6}+\frac{3 {{l}^{3}} q\, {{x}^{2}}}{2}+6 F\, {{l}^{2}}\, {{x}^{2}}}{6 E I l}+\frac{\left( 37 {{l}^{3}} q+176 F\, {{l}^{2}}+36 M l\right) x}{72 E I}... \]
\[ \tag{53} ...-\frac{{{l}^{4}} q+32 F\, {{l}^{3}}}{24 E I} \]
Die Ermittlung der Biegelinien ist damit abgeschlossen. Es ist deutlich zu erkennen, dass bei der Verwendung des gleichen Koordinatenursprungs in den Bereichen I bis III sehr umfangreiche Formeln entstehen. Eine Vereinfachung kann erreicht werden, indem bspw. im dritten Bereich eine Ersatzkoordinate eingeführt wird, die entgegengesetzt zur ursprünglichen x-Richtung läuft und bei x = 3l beginnt.
Werbung




