This exercise is about the determination of the stress vector and section plane for a given stress state and normal vector.
Task
The following stress tensor is given at a point in space in the cartesian coordinate system:
\[ \newcommand{\myvec}[1]{{\begin{bmatrix}#1\end{bmatrix}}} \]\[ S = \myvec{1 & 2 & -2\\2 & 1 & 2\\-2 & 2 & 1} \cdot 100 \, Nmm^{-2} \]
Sought are
a) the stress vector to the plane described through the normal unit vector
\[ \newcommand{\myvec}[1]{{\begin{bmatrix}#1\end{bmatrix}}} \]\[ \vec{n} = \frac{1}{3} \cdot \myvec{-2\\1\\2} \]
b) the absolute value of the stress vector calculated in a) and
c) the equation that determines the section plane given by the normal unit vector.
Solution
\[ \newcommand{\myvec}[1]{{\begin{bmatrix}#1\end{bmatrix}}} \]a) Calculation of the stress vector
The stress vector is calculated with the Cauchy stress equation:
\[ \tag{1} \vec{S} = S \cdot \vec{n} \]
\[ \tag{2} \vec{S} = \myvec{1 & 2 & -2\\2 & 1 & 2\\-2 & 2 & 1} \cdot \myvec{-2\\1\\2} \cdot \frac{1}{3} \cdot 100 \, Nmm^{-2} \]
\[ \tag{3} \vec{S} = \myvec{-4\\1\\0} \cdot \frac{100}{3} Nmm^{-2} \]
b) Absolute value of the stress vector
The absolute value of the stress vector follows from
\[ \tag{4} | \vec{S} | = \sqrt{S_x^2+S_y^2+S_z^2} \]
\[ \tag{5} | \vec{S} | = \sqrt{-4^2+1^2+0^2} \cdot \frac{100}{3} Nmm^{-2} \]
\[ \tag{6} | \vec{S} | = 137,4 \, Nmm^{-2} \]
\[ \newcommand{\myvec}[1]{{\begin{bmatrix}#1\end{bmatrix}}} \] \[ \require{cancel} \]c) Equation for the plane from the normal vector
The general equation for a plane derived from a normal vector is
\[ \tag{7} a\cdot x + b\cdot y +c \cdot z = 0 \]
with the components of the normal vector (the given 1/3 can be neglected for the plane equation )
\[ \tag{8} \vec{n} = \myvec{a\\b\\c} \cdot \bcancel{\frac{1}{3}}\]
Thus the equation for the section plane is
\[ \tag{9} -2x + y + 2z = 0 \]
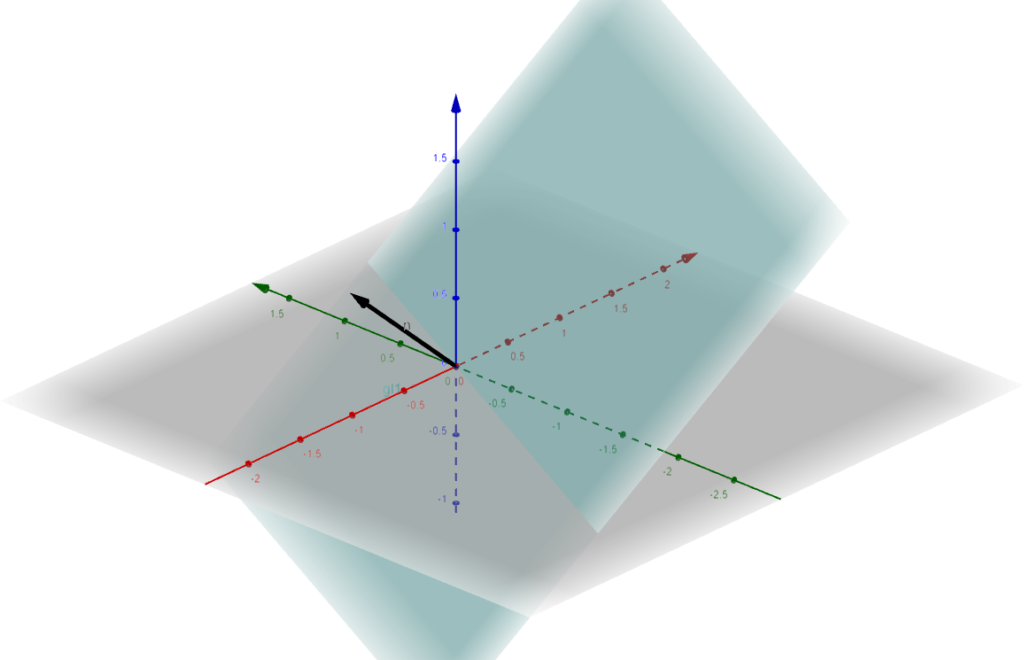
So the stress vector and section plane have been determined. Feel free to navigate through the other exercises as shown in the categories.

