This exercise is about the stand up condition of a tumbler and addresses the following questions:
- How to describe a geometrical shape as a function?
- How to calculate the area of a geometrical shape using integration?
- How to calculate the area of a semicircle using polar coordinates?
- How to calculate the center of gravity for a triangle?
- How to calculate the center of gravity for a semicircle?
- How to express an imbalance as a formula?
Task
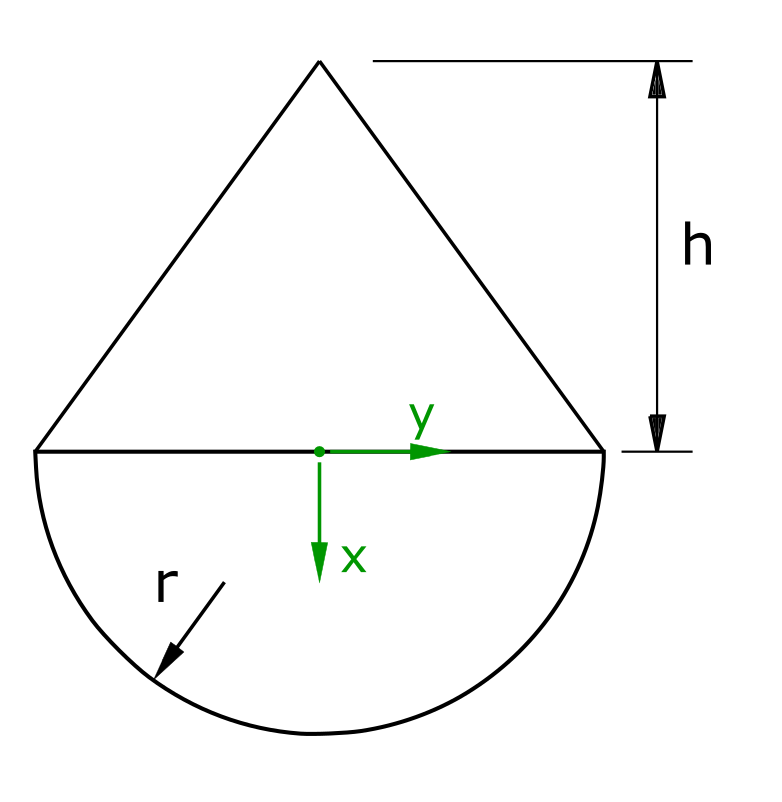
A tumbler consists of a semicircular surface with the radius r and a triangular surface with the height h placed on it. The ratio of h to r has to be calculated so that the tumbler stands up. Friction should not be taken into account here.
Solution
To solve the task, the first step is to calculate the respective individual areas and individual centroids. Then the stand up condition is formulated and solved. To simplify the calculation, the coordinate direction for x is assumed to be positive for the semicircle and the triangle.
Due to the symmetry of the tumbler around the x-axis, the coordinates of the centroids are only considered along the x-axis.
Area of the semicircle
The area of the semicircle is referred to as A1. Since it is only possible to calculate the area of the semicircle in Cartesian coordinates with great effort, polar coordinates are used here.
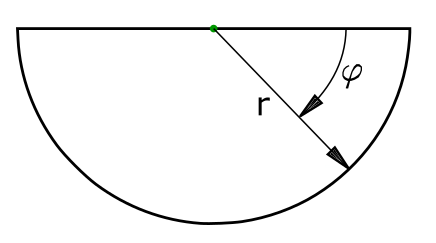
\[ \tag{1} A_1 = \int\limits_0^\pi \int\limits_0^r r \, dr \, d \phi \]
\[ \tag{2} A_1 = \int\limits_0^\pi \frac{r^2}{2} d \phi \]
\[ \tag{3} A_1 = \frac{\pi \cdot r^2}{2} \]
Centroid of the semicircle
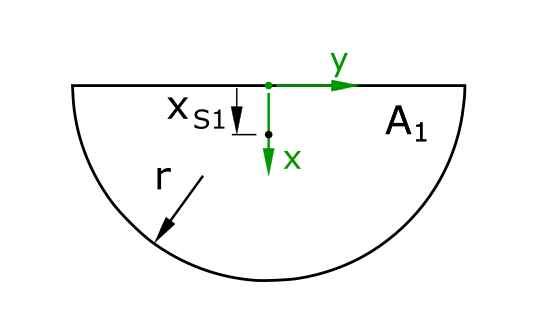
The center of gravity coordinate of the semicircle is designated as xS1. It should be noted here that the sine and cosine functions in the calculation of the x and y coordinates must be adapted to the respective coordinate system. In this case, the sine function is to be used for the x component searched for here.
\[ \require{cancel} \]\[ \tag{4} x_{S1} = \frac{\int\limits_0^\pi \int\limits_0^r r^2 \cdot sin \phi \, dr \, d \phi}{A_1} \]
\[ \tag{5} x_{S1} = \frac{\int\limits_0^\pi \frac{r^3}{3} \cdot sin \phi \,d \phi}{\frac{\pi \cdot r^2}{2}} \]
\[ \tag{6} x_{S1} = \frac{\frac{2 \cdot r^3}{3}}{\frac{\pi \cdot r^2}{2}} \]
\[ \tag{7} x_{S1} = \frac{4 \cdot r}{3 \cdot \pi} \]
Area of the triangle
The area of the triangle is called A2. The area A2 is calculated over the width as a function of x.
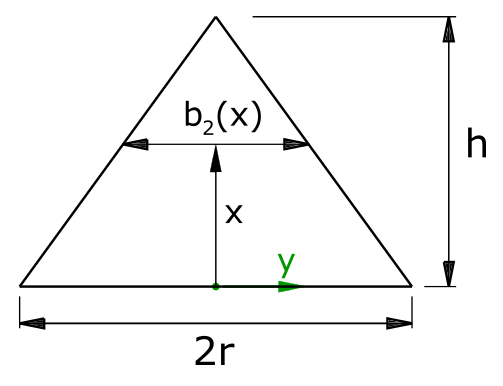
The width b2(x) can be formulated as follows:
\[ \tag{8} b_2(x) = 2 \cdot r \cdot (1- \frac{x}{h}) \]
The area A2 results from this
\[ \tag{9} A_2 = \int\limits_0^h{2 \cdot r \cdot (1- \frac{x}{h})dx} \]
\[ \tag{10} A_2 = h \cdot r \]
Center of gravity of the triangle
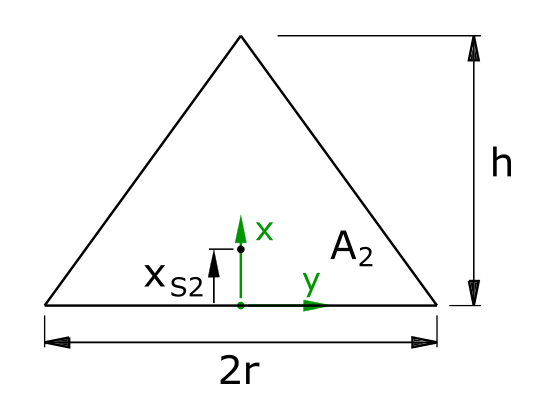
The center of gravity coordinate of the triangle is referred to as xS2.
\[ \tag{11} x_{S2} = \frac{\int\limits_0^h{2 \cdot r \cdot (1- \frac{x}{h})\cdot x \,dx}}{A_2} \]
\[ \tag{12} x_{S2} = \frac{\frac{h^2 \cdot r}{3}}{h \cdot r} \]
\[ \tag{13} x_{S2} = \frac{h}{3} \]
All the required sizes of the two surfaces are thus determined.
Erecting condition
In order for the tumbler coming up, the product of the area of the circle and its center of gravity must be greater than the product of the area of the triangle and its center of gravity.
\[ \require{cancel} \]\[ \tag{14} x_{S1} \cdot A_1 > x_{S2} \cdot A_2 \]
\[ \tag{15} \frac{4 \cdot r}{3 \cdot \pi} \cdot \frac{\pi \cdot r^2}{2} > \frac{h}{3} \cdot h \cdot r \]
\[ \tag{16} 2 \cdot r^2 > h^2 \]
\[ \tag{17} \frac{h}{r} < \sqrt{2} \]
So the stand up condition of the tumbler has been found.

