This exercise is about the following questions:
- How to calculate the center of gravity of a hemisphere in cartesian coordinates?
- How is the formula for the center of gravity of a hemisphere derived?
In the solution below, the formula for the area of a circular area is assumed to be known.
Task
For a hemisphere with the radius R, the center of gravity coordinate in the x direction has to be calculated.
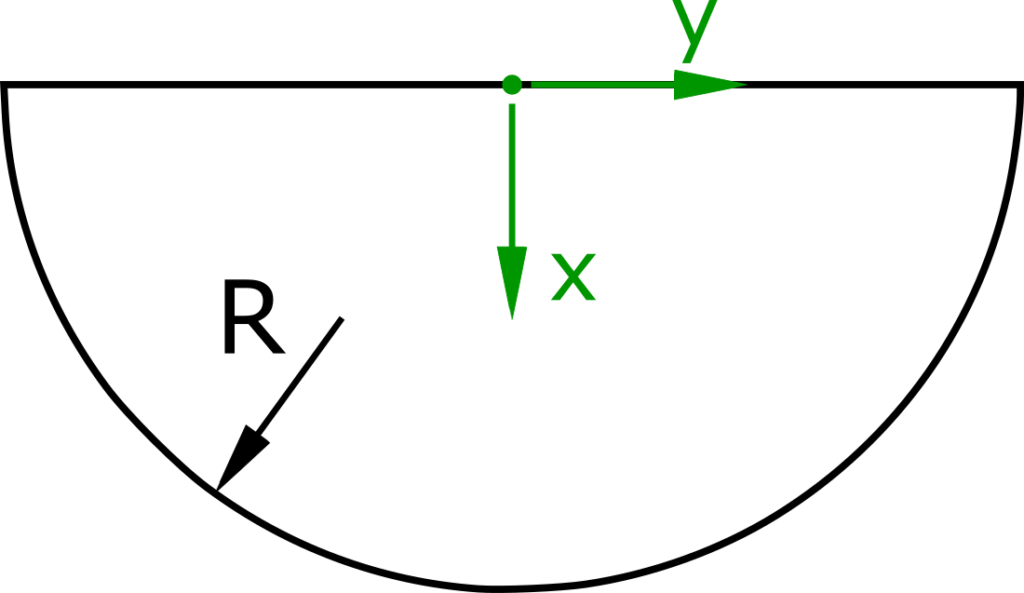
Solution
In the solution shown here the result is calculated with cartesian coordinates.
The following sketch shows the geometrical relationships for calculating the face A(x) or the radius r(x). The face A(x) lays in the y-z-plane. The product A(x)dx represents the volume element or elements that are added up.
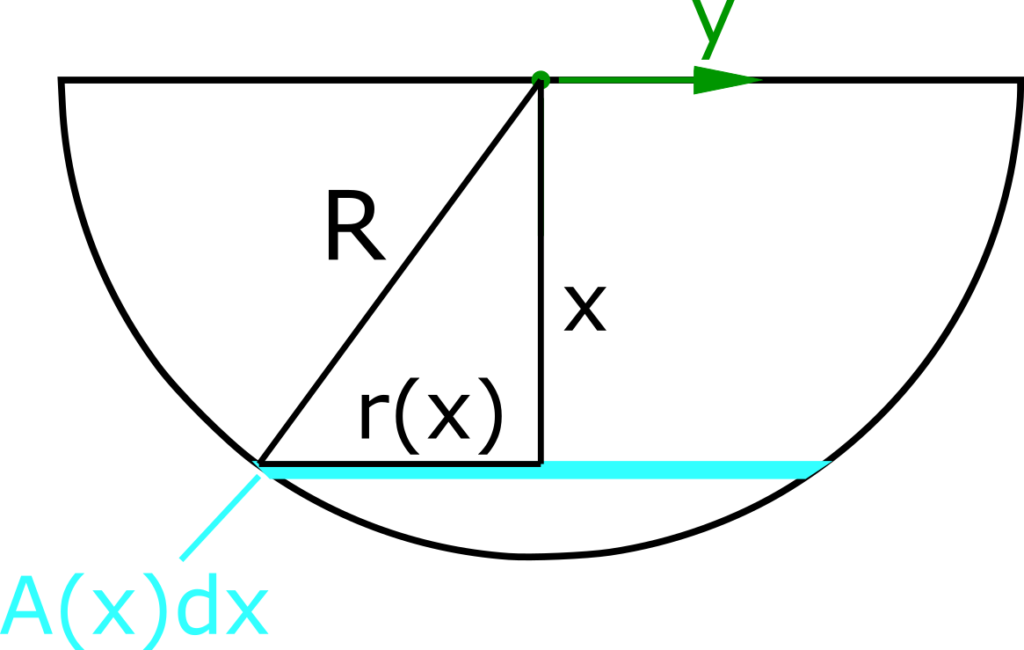
To calculate the center of gravity, the volume of the hemisphere is calculated first. This is done by integrating over the cross-sectional area along the x coordinate. The area of the circle is known to be:
\[ \tag{1} A = \pi \cdot r^2 \]
The radius r of the cross-sectional area depends on x and can be expressed as follows:
\[ \tag{2} r(x) = \pi \cdot \sqrt{R^2-x^2} \]
So that is the cross section
\[ \tag{3} A(x) = \pi \cdot \left( R^2-x^2 \right) \]
The volume of the hemisphere is
\[ \tag{4} V = \int\limits_0^R{\pi \cdot \left( R^2-x^2 \right) dx} \]
\[ \tag{4.1} V = \left[ \pi \cdot \left( R^2 \cdot x - \frac{1}{3} \cdot x^3 \right) \right]_0^R \]
\[ \tag{4.2} V = \left[ \pi \cdot \left( R^2 \cdot R - \frac{1}{3} \cdot R^3 \right) \right] - \bcancel{\left[ \pi \cdot \left( R^2 \cdot 0 - \frac{1}{3} \cdot 0^3 \right) \right]} \]
\[ \tag{5} V = \frac{2}{3} \cdot \pi \cdot R^3 \]
The center of gravity coordinate xS is calculated as follows
\[ \tag{6} x_S = \frac{\int\limits_0^R{\pi \cdot \left( R^2-x^2 \right) \cdot x \, dx}}{V} \]
\[ \tag{6.1} x_S = \frac{\left[ \pi \cdot \left( \frac{1}{2} \cdot R^2 \cdot x^2 - \frac{1}{4} \cdot x^4 \right) \right]_0^R}{\frac{2}{3} \cdot \pi \cdot R^3} \]
\[ \tag{6.2} x_S = \frac{\left[ \pi \cdot \left( \frac{1}{2} \cdot R^2 \cdot R^2 - \frac{1}{4} \cdot R^4 \right) \right] - \bcancel{ \left[ \pi \cdot \left( \frac{1}{2} \cdot R^2 \cdot 0^2 - \frac{1}{4} \cdot 0^4 \right) \right]}}{\frac{2}{3} \cdot \pi \cdot R^3} \]
\[ \tag{6.3} x_S = \frac{ \frac{3}{4} \cdot \pi \cdot R^4 }{2 \cdot \pi \cdot R^3} \]
from which follows
\[ \tag{7} x_S = \frac{3}{8} \cdot R \]

