Werbung
Diese Übung behandelt folgende Fragen:
- Wie berechnet man den Schwerpunkt einer Halbkugel in kartesischen Koordinaten?
- Wie wird die Formel für den Schwerpunkt einer Halbkugel hergeleitet?
In der unten aufgeführten Lösung wird die Formel für den Flächeninhalt einer Kreisfläche als bekannt vorausgesetzt.
Aufgabe
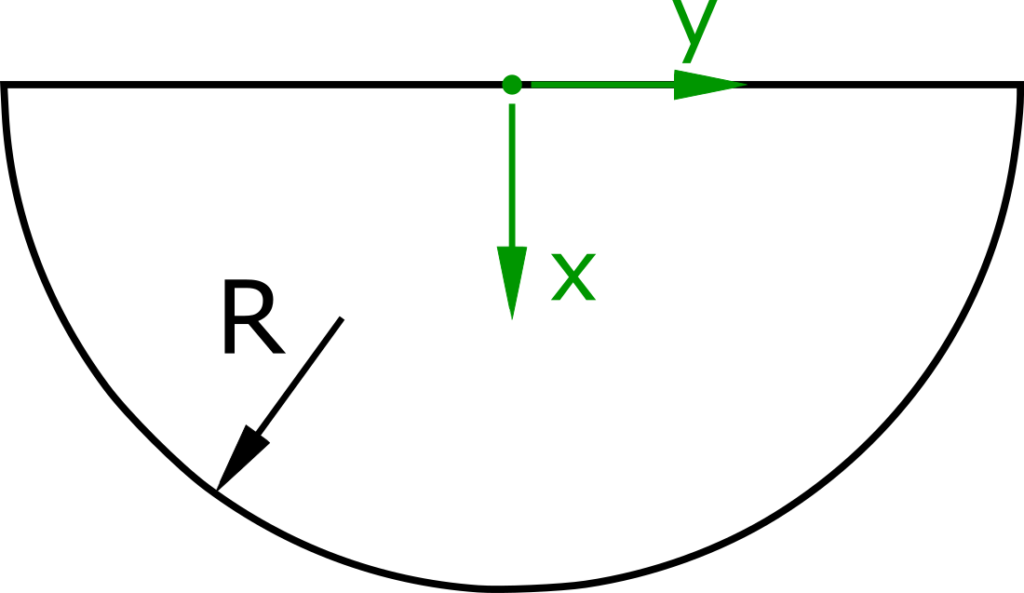
Für eine Halbkugel mit dem Radius R ist die Schwerpunktkoordinate in x-Richtung zu berechnen.
Lösung
In der hier gezeigten Lösung wird mit kartesischen Koordinaten gearbeitet.
Die nachfolgende Skizze zeigt die geometrischen Zusammenhänge zur Berechnung der Fläche A(x) bzw. des Radius r(x). Die Fläche A(x) liegt in der y-z-Ebene. Das Produkt A(x)dx stellt das bzw. die Volumenelemente dar, die aufsummiert werden.
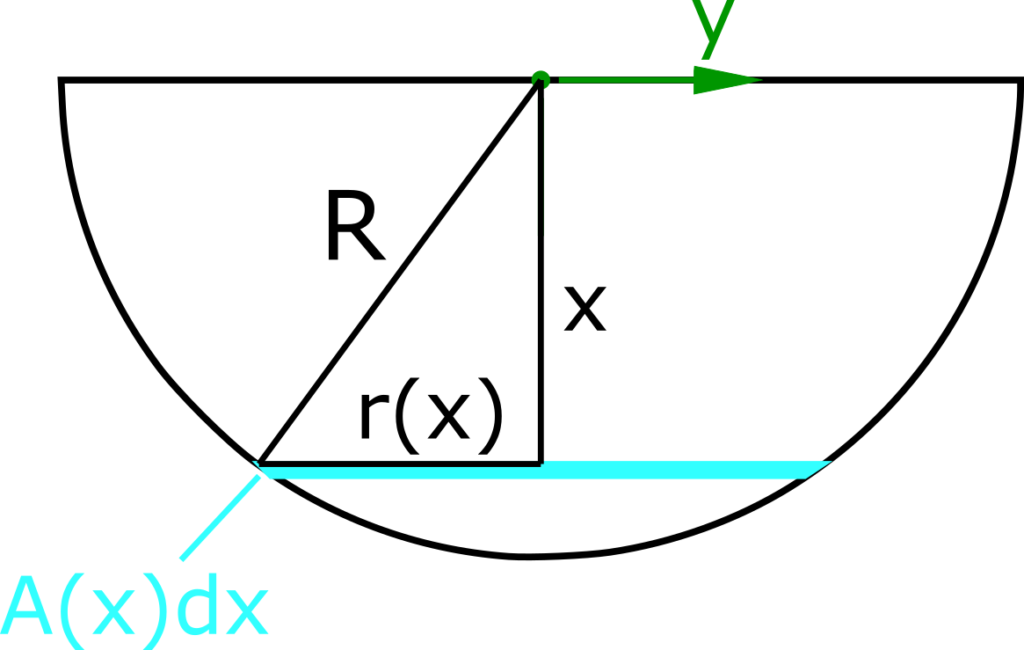
Zur Berechnung des Schwerpunkts wird zuerst das Volumen der Halbkugel berechnet. Dies erfolgt, in dem über die Querschnittsfläche entlang der Koordinate x integriert wird. Die Fläche des Kreises beträgt bekanntermaßen:
\[ \tag{1} A = \pi \cdot r^2 \]
Der Radius r der Querschnittsfläche ist abhängig von x und kann wie folgt ausgedrückt werden:
\[ \tag{2} r(x) = \pi \cdot \sqrt{R^2-x^2} \]
Damit ist der Querschnitt
\[ \tag{3} A(x) = \pi \cdot \left( R^2-x^2 \right) \]
Das Volumen der Halbkugel beträgt
\[ \tag{4} V = \int\limits_0^R{\pi \cdot \left( R^2-x^2 \right) dx} \]
\[ \tag{4.1} V = \left[ \pi \cdot \left( R^2 \cdot x - \frac{1}{3} \cdot x^3 \right) \right]_0^R \]
\[ \tag{4.2} V = \left[ \pi \cdot \left( R^2 \cdot R - \frac{1}{3} \cdot R^3 \right) \right] - \bcancel{\left[ \pi \cdot \left( R^2 \cdot 0 - \frac{1}{3} \cdot 0^3 \right) \right]} \]
\[ \tag{5} V = \frac{2}{3} \cdot \pi \cdot R^3 \]
Die Schwerpunktkoordinate xS wird wie folgt berechnet
\[ \tag{6} x_S = \frac{\int\limits_0^R{\pi \cdot \left( R^2-x^2 \right) \cdot x \, dx}}{V} \]
\[ \tag{6.1} x_S = \frac{\left[ \pi \cdot \left( \frac{1}{2} \cdot R^2 \cdot x^2 - \frac{1}{4} \cdot x^4 \right) \right]_0^R}{\frac{2}{3} \cdot \pi \cdot R^3} \]
\[ \tag{6.2} x_S = \frac{\left[ \pi \cdot \left( \frac{1}{2} \cdot R^2 \cdot R^2 - \frac{1}{4} \cdot R^4 \right) \right] - \bcancel{ \left[ \pi \cdot \left( \frac{1}{2} \cdot R^2 \cdot 0^2 - \frac{1}{4} \cdot 0^4 \right) \right]}}{\frac{2}{3} \cdot \pi \cdot R^3} \]
\[ \tag{6.3} x_S = \frac{ \frac{3}{4} \cdot \pi \cdot R^4 }{2 \cdot \pi \cdot R^3} \]
woraus sich ergibt
\[ \tag{7} x_S = \frac{3}{8} \cdot R \]
Werbung




