Werbung
Diese Übung beschäftigt sich mit folgenden Fragen:
- Wie stellt man eine Funktion für die Beschreibung einer geometrischen Form auf?
- Wie berechnet man den Flächeninhalt mit dem Integral einer Funktion?
- Wie berechnet man eine Halbkreisfläche in Polarkoordinaten?
- Wie berechnet man den Schwerpunkt eines Dreiecks?
- Wie berechnet man den Schwerpunkt eines Halbkreises?
- Wie formuliert man ein Ungleichgewicht als Formel?
Aufgabe
Ein Stehaufmännchen besteht aus einer Halbkreisfläche mit dem Radius r und einer darauf aufgesetzten Dreiecksfläche mit der Höhe h. Es ist das Verhältnis von h zu r zu berechnen, damit sich das Stehaufmännchen aufrichtet. Reibung soll hierbei nicht berücksichtigt werden.
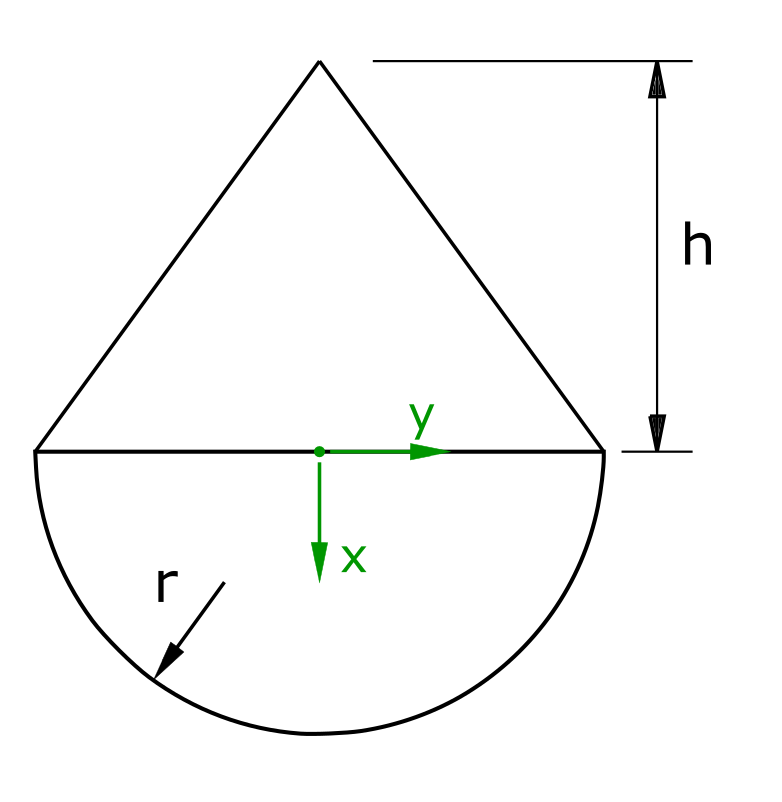
Lösung
Zur Lösung der Aufgabe werden im ersten Schritt die jeweiligen Einzelflächen und Einzelschwerpunkte berechnet. Anschließend wird die Aufrichtbedingung formuliert und gelöst. Um die Berechnung zu vereinfachen, wird die Koordinatenrichtung für x in beiden Fällen positiv angenommen.
Die Betrachtung der Schwerpunktkoordinaten erfolgt aufgrund der Symmetrie des Stehaufmännchens um die x-Achse nur entlang der x-Achse.
Flächeninhalt des Halbkreises
Die Fläche des Halbkreises wird als A1 bezeichnet. Da eine Berechnung der Fläche des Halbkreises in kartesischen Koordinaten nur mit großem Aufwand möglich ist, werden hier Polarkoordinaten verwendet.
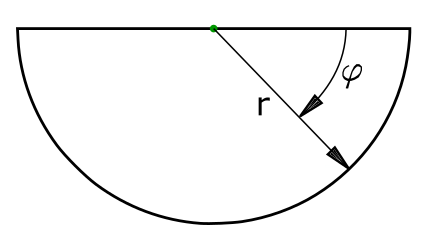
\[ \tag{1} A_1 = \int\limits_0^\pi \int\limits_0^r r \, dr \, d \phi \]
\[ \tag{2} A_1 = \int\limits_0^\pi \frac{r^2}{2} d \phi \]
\[ \tag{3} A_1 = \frac{\pi \cdot r^2}{2} \]
Schwerpunkt der Halbkreises
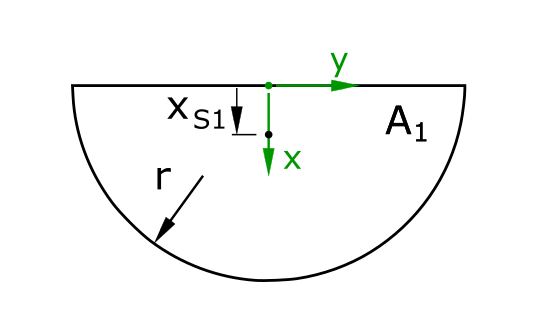
Die Schwerpunktkoordinate des Halbkreises wird als xS1 bezeichnet. Zu beachten ist hier, dass die Sinus- und Kosinusfunktion in der Berechnung der x- und y-Koordinate auf das jeweilige Koordinatensystem angepasst sein muss. In diesem Fall ist für die hier gesuchte x-Komponente die Sinusfunktion zu verwenden.
\[ \require{cancel} \]\[ \tag{4} x_{S1} = \frac{\int\limits_0^\pi \int\limits_0^r r^2 \cdot sin \phi \, dr \, d \phi}{A_1} \]
\[ \tag{5} x_{S1} = \frac{\int\limits_0^\pi \frac{r^3}{3} \cdot sin \phi \,d \phi}{\frac{\pi \cdot r^2}{2}} \]
\[ \tag{6} x_{S1} = \frac{\frac{2 \cdot r^3}{3}}{\frac{\pi \cdot r^2}{2}} \]
\[ \tag{7} x_{S1} = \frac{4 \cdot r}{3 \cdot \pi} \]
Flächeninhalt des Dreiecks
Die Fläche des Dreiecks wird als A2 bezeichnet. Die Fläche A2 wird über die Breite in Abhängigkeit von x berechnet.
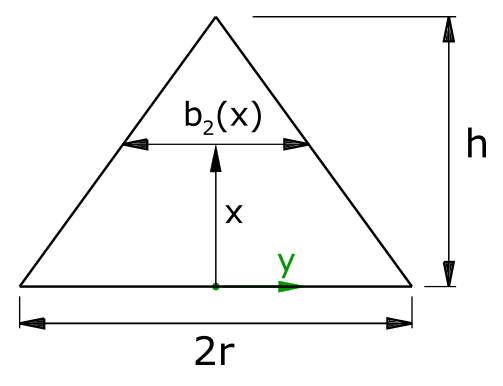
Die Breite b2(x) lässt sich wie folgt formulieren:
\[ \tag{8} b_2(x) = 2 \cdot r \cdot (1- \frac{x}{h}) \]
Die Fläche A2 ergibt sich damit aus
\[ \tag{9} A_2 = \int\limits_0^h{2 \cdot r \cdot (1- \frac{x}{h})dx} \]
\[ \tag{10} A_2 = h \cdot r \]
Schwerpunkt des Dreiecks
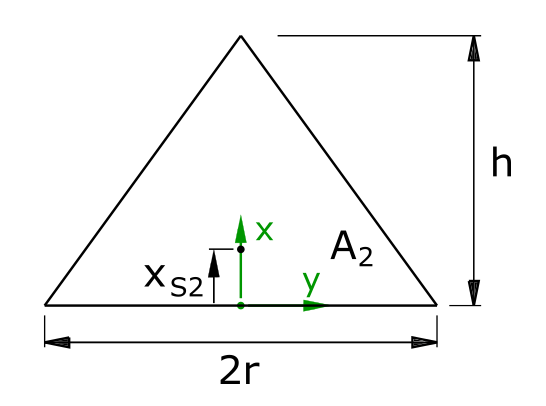
Die Schwerpunktkoordinate des Dreiecks wird als xS2 bezeichnet.
\[ \tag{11} x_{S2} = \frac{\int\limits_0^h{2 \cdot r \cdot (1- \frac{x}{h})\cdot x \,dx}}{A_2} \]
\[ \tag{12} x_{S2} = \frac{\frac{h^2 \cdot r}{3}}{h \cdot r} \]
\[ \tag{13} x_{S2} = \frac{h}{3} \]
Damit sind alle erforderlichen Größen der beiden Flächen bestimmt.
Aufrichtbedingung
Damit sich das Stehaufmännchen aufrichtet, muss der Produkt aus Kreisfläche und Kreisschwerpunkt größer sein als das Produkt aus Dreiecksfläche und Dreiecksschwerpunkt.
\[ \require{cancel} \]\[ \tag{14} x_{S1} \cdot A_1 > x_{S2} \cdot A_2 \]
\[ \tag{15} \frac{4 \cdot r}{3 \cdot \pi} \cdot \frac{\pi \cdot r^2}{2} > \frac{h}{3} \cdot h \cdot r \]
\[ \tag{16} 2 \cdot r^2 > h^2 \]
\[ \tag{17} \frac{h}{r} < \sqrt{2} \]
Werbung




