Task
The center of gravity has to be calculated for the body shown. The body consists of two individual bodies of different materials.
Given values:
a = 30 mm, b = 25 mm, c = 60 mm, d = 30 mm, e = 50 mm
Body 1 consists of steel with a density of ρ = 7.850 kg/m³,
Body 2 is made of aluminium with a density of ρ = 2.660 kg/m³.
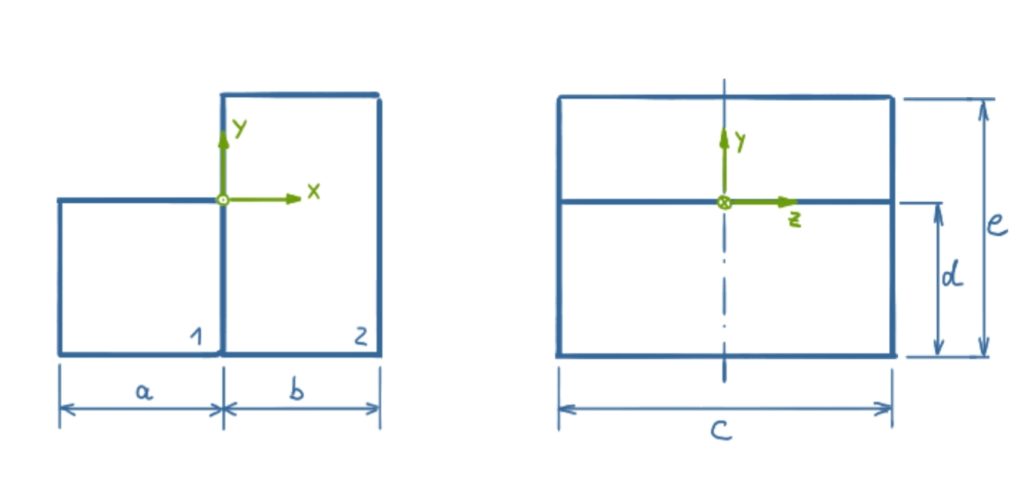
A note on the direction of projection: a circle with a center point indicates a coordinate axis that points at the viewer. A circle with a cross is a coordinate axis that points away from the viewer.
Solution
\[ \require{cancel} \]The equation for calculating the center of gravity coordinate is, noted here as an example for x S :
\[ \tag{1} x_S = \frac{\sum \rho_i \cdot V_i \cdot x_i}{\sum \rho_i \cdot V_i} \]
The values of the individual bodies are recorded in a table
| \[ i \] | \[ V_i \] | \[ x_i \] | \[ y_i \] | \[ z_i \] | \[ \rho_i \] | \[ \rho_i \cdot V_i \] | \[ \rho_i \cdot V_i \cdot x_i \] | \[ \rho_i \cdot V_i \cdot y_i \] | \[ \rho_i \cdot V_i \cdot z_i \] |
|---|---|---|---|---|---|---|---|---|---|
| \[ {mm}^3 \] | \[ mm \] | \[ mm \] | \[ mm \] | \[ 10^{-6}kg/{mm}^3 \] | \[ kg \] | \[ kgmm \] | \[ kgmm \] | \[ kgmm \] | |
| 1 | 54.000 | -15 | -15 | 0 | 7,85 | 0,424 | -6,359 | -6,359 | 0 |
| 2 | 75.000 | 12,5 | -5 | 0 | 2,66 | 0,2 | 2,494 | -0,998 | 0 |
| \[ \sum \] | 0,624 | -3,865 | -7,357 | 0 |
This results in the following center of gravity coordinates:
\[ \tag{2} x_S = \frac{-3.865 kg\,mm}{0.624kg} = -6.2\,mm \]
\[ \tag{3} y_S = \frac{-7.357 kg\,mm}{0.624kg} = -11.8\,mm \]
\[ \tag{4} z_S = \frac{0 kg\,mm}{0.624kg} = 0\,mm \]
So the center of gravity of the combined body is determined.

