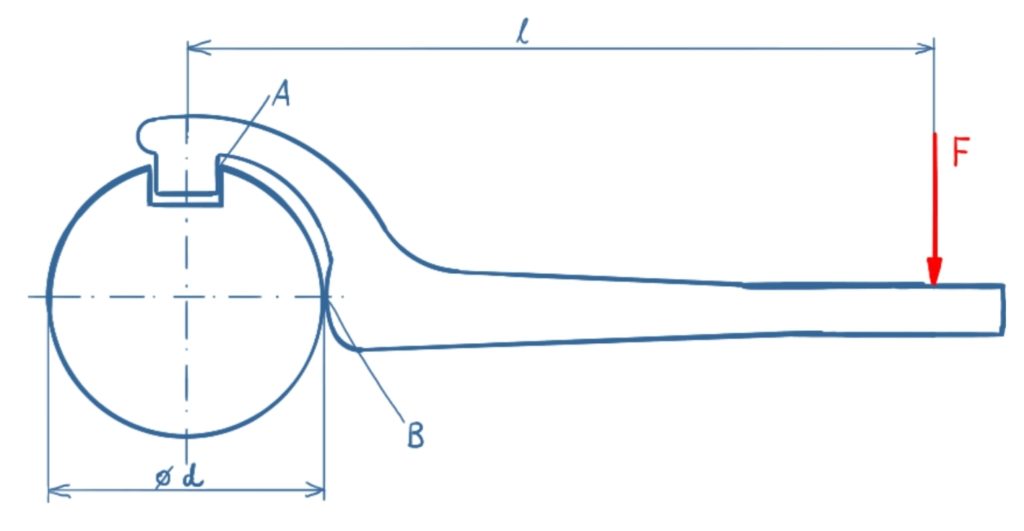
Task
A hook wrench is attached to a stationary shaft. Which reaction forces arise in A and B under the assumption that the contact in B is frictionless?
Solution
The following video is in german language. Please scroll down for the written solution.
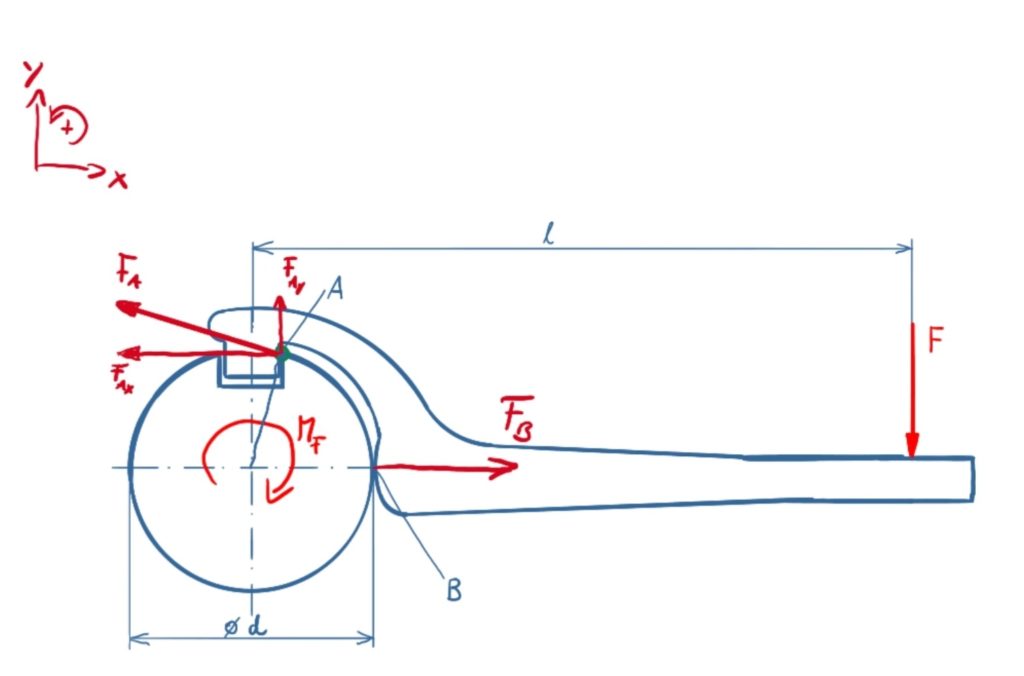
The reaction forces on the shaft are shown in the sketch of the solution. The hook wrench touches the shaft at points A and B. On a spatial shaft a line contact would occur.
The equilibrium of forces in the x-direction is
\[\tag{1} \sum F_x = 0 = F_B - F_{Ax} \]
\[\tag{2} F_{Ax} = F_B \]
The equilibrium of forces in the y-direction is
\[\tag{3} \sum F_y = 0 = F_{Ay} - F \]
\[\tag{4} F_{Ay} = F \]
The equilibrium of moments is established around the axis of rotation of the shaft. The moment applied by the force F is referred to as M F , so that the moment equilibrium reads
\[\tag{5} \sum M = 0 = - M_F + F_A \cdot \frac{d}{2} \]
\[\tag{6} F_A \cdot \frac{d}{2} = F \cdot l \]
\[\tag{7} F_A = \frac{2 \cdot F \cdot l}{d} \]
The still unknown horizontal forces are calculated using the Pythagorean theorem:
\[\tag{8} F_A^2 = F_{Ax}^2 + F_{Ay}^2 \]
\[\tag{9} \left( \frac{2 \cdot F \cdot l}{d} \right)^2 = F_{Ax}^2 + F^2 \]
\[\tag{10} F_{Ax} = \sqrt{\left( \frac{2 \cdot F \cdot l}{d} \right)^2 - F^2} \]

