A click on the respective picture leads to the calculation of the centroids:
General information and exercises for calculating centroids can be found under the respective keyword.
Centers of area in the plane
Triangle
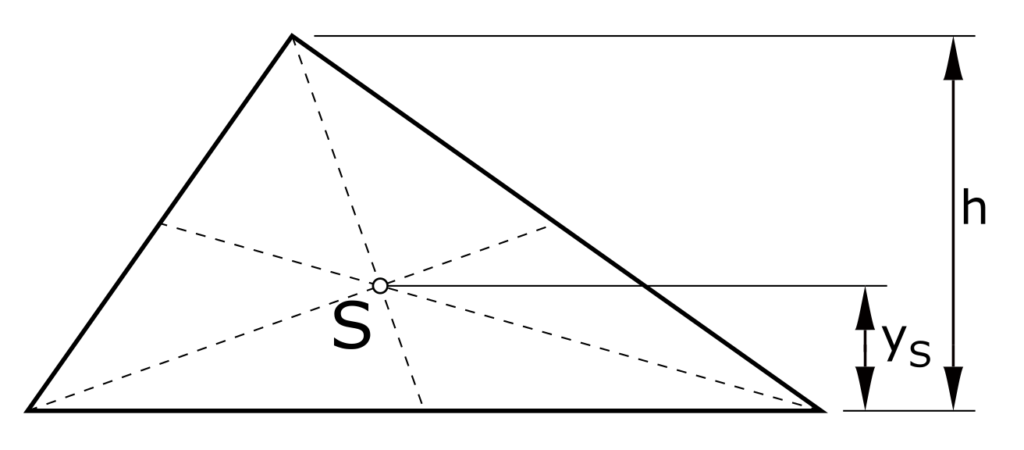
\[ y_S = \frac{h}{3}\]
Parallelogram
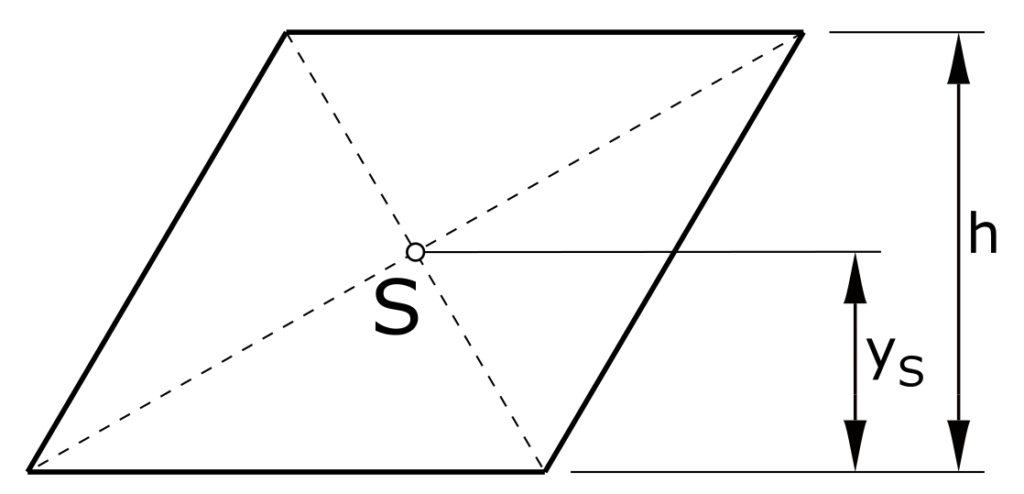
\[ y_S = \frac{h}{2}\]
Trapezoid
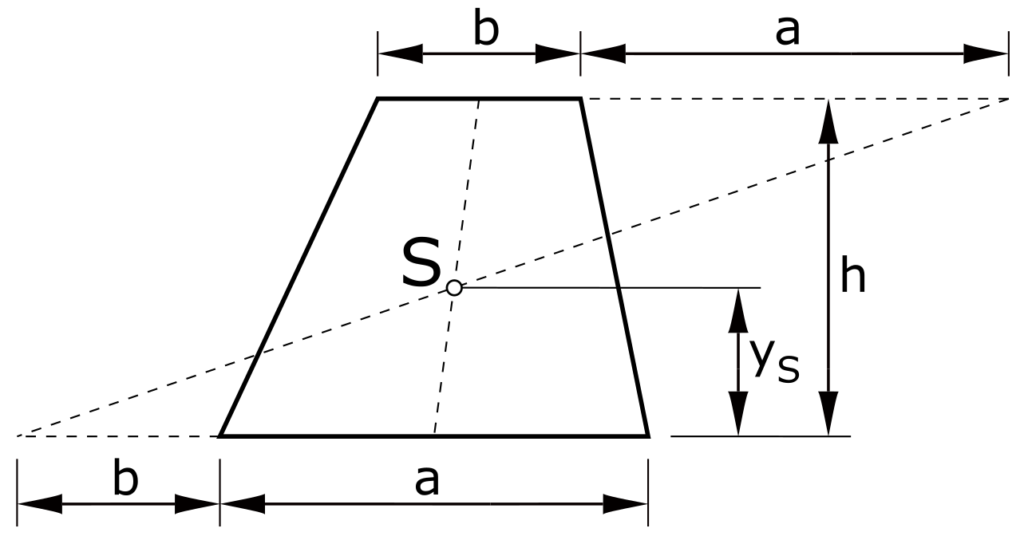
\[ y_S = \frac{h}{3} \cdot \frac{a+2\cdot b}{a+b}\]
Circle section
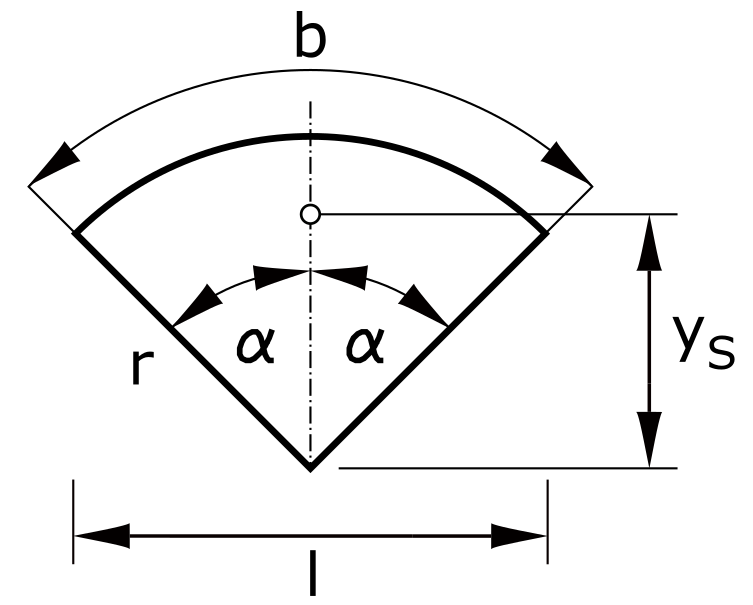
\[ y_S = \frac{2 \cdot r \cdot sin \alpha}{3 \cdot \alpha}\]
\[ y_S = \frac{2 \cdot r \cdot l}{3 \cdot b}\]
For the semicircle it is
\[ y_S = \frac{4 \cdot r }{3 \cdot \pi}\]
Circle segment
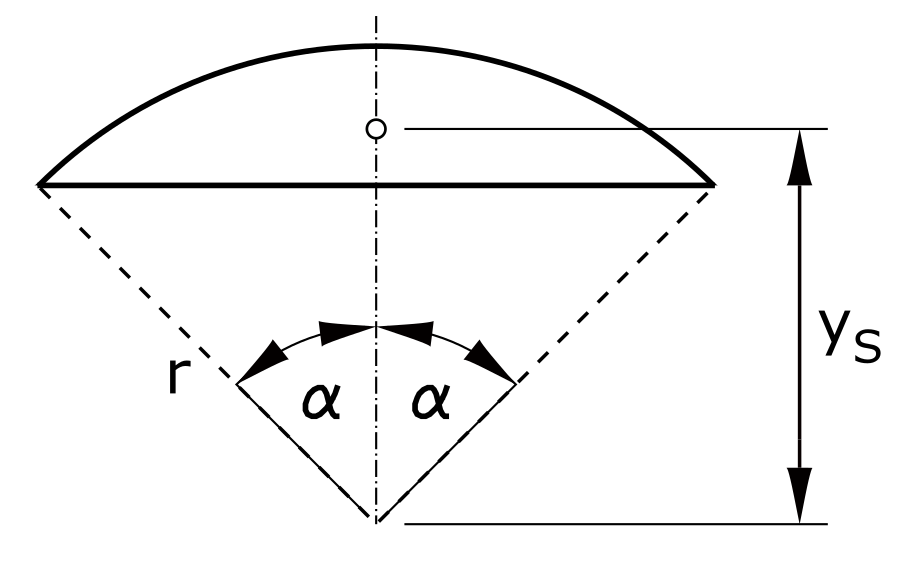
\[ y_S = \frac{2}{3} \cdot \frac{r \cdot sin^3 \alpha}{\alpha - sin \alpha \cdot cos \alpha} \]
For the semicircle it is
\[ y_S = \frac{4 \cdot r }{3 \cdot \pi}\]
Circular ring section
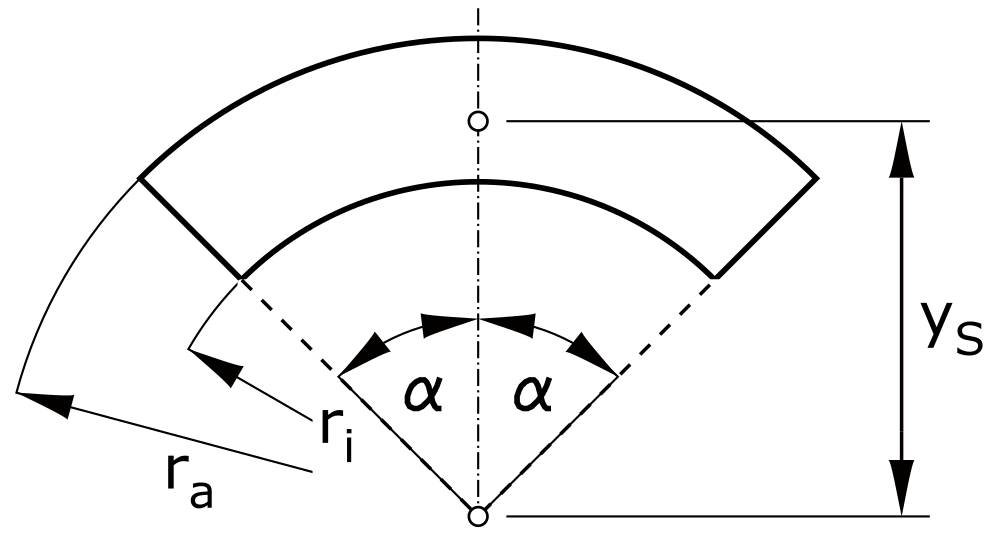
\[ y_S = \frac{2}{3} \cdot \frac{\left( r_a^3-r_i^3 \right) \cdot sin \alpha}{\left( r_a^2-r_i^2\right) \cdot \alpha} \]
Parabolic surfaces
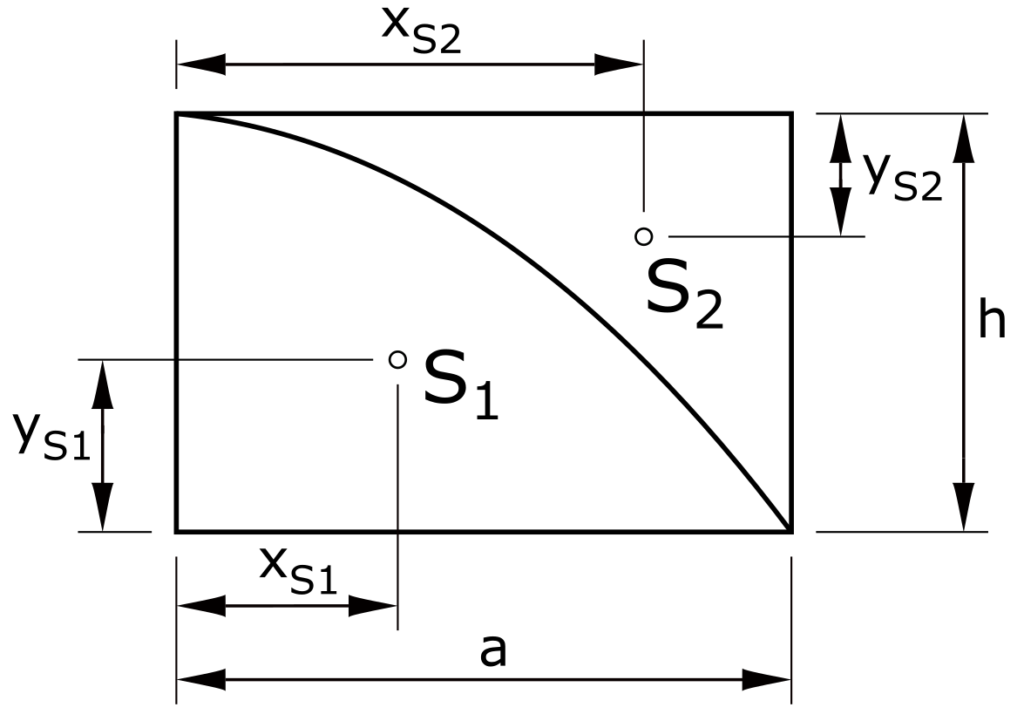
Centroid S1
\[ x_{S1} = \frac{3 \cdot a}{8} \]
\[ y_{S1} = \frac{2 \cdot h}{5} \]
Centroid S2
\[ x_{S2} = \frac{3 \cdot a}{4} \]
\[ y_{S2} = \frac{3 \cdot h}{10} \]
Parabolic section
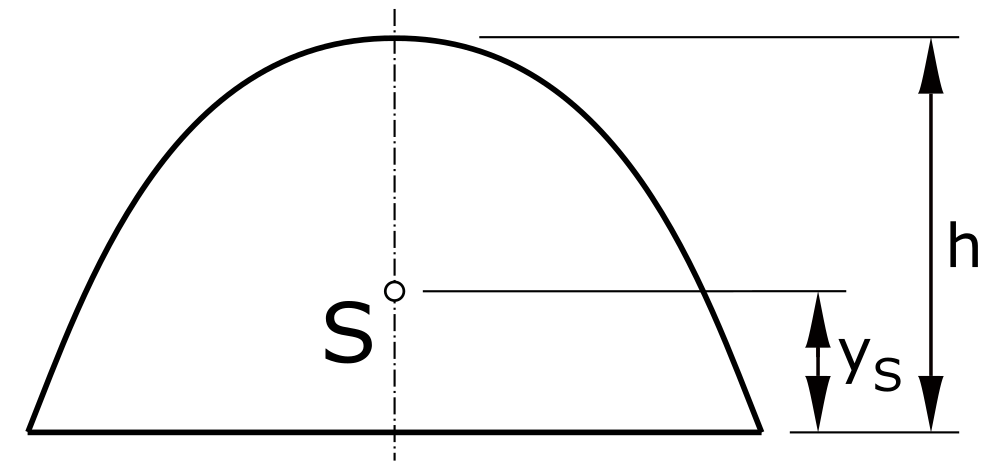
\[ y_S = \frac{2 \cdot h}{5} \]
Elliptical section
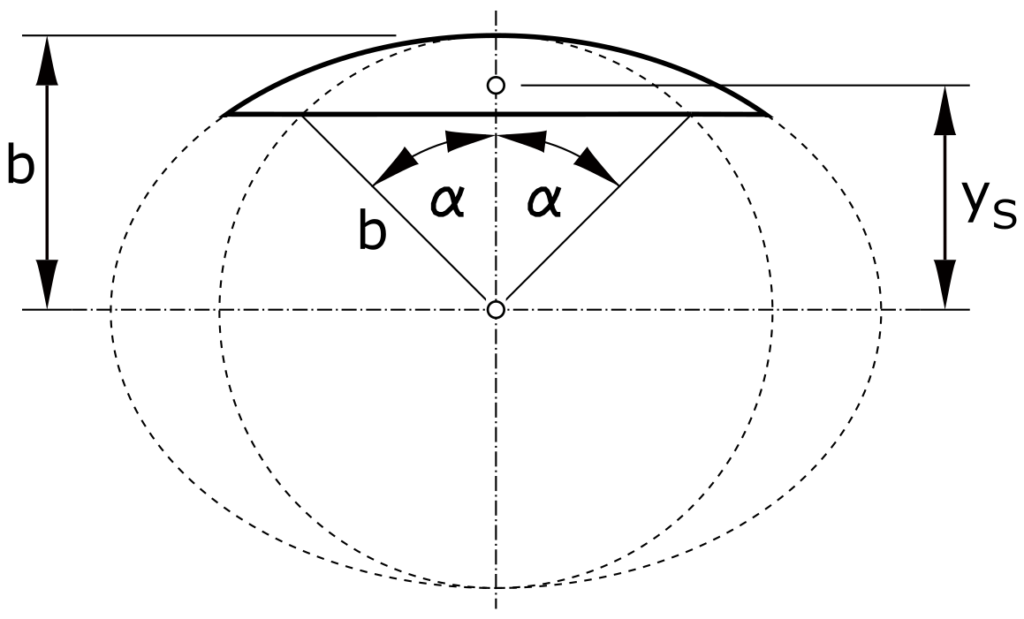
\[ y_S = \frac{2 }{3} \cdot \frac{b \cdot sin^3 \alpha}{\alpha - sin \alpha \cdot cos \alpha} \]

