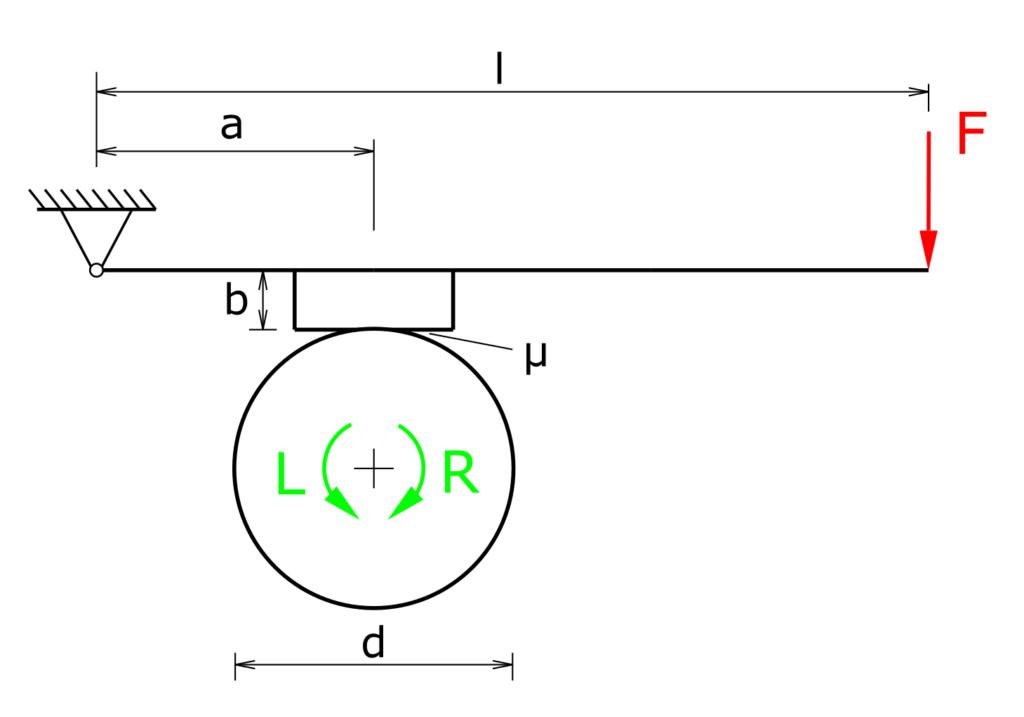
This exercise is about the determination of drum braking torques in different rotation directions. See an example for this kind of brakes here.
Task
A drum is braked with a brake pad that is pressed on with an operating lever. The drum can be operated in both left and right rotation.
a) What drum braking torques are achieved for left and right rotation?
b) What value does the height b must have so that the braking torques for right and left rotation are the same?
c) At what height b does the brake “seize”? Does this happen in clockwise or counterclockwise rotation?
Solution
The following video is in German language, but English subtitles are available.
Determination of the drum braking torques
The two braking torques for clockwise and counter-clockwise rotation are calculated from the friction force FBx and half the drum diameter.
\[ M_{BL}=-F_{Bx} \cdot \frac{d}{2} \]
\[ M_{BR}=F_{Bx} \cdot \frac{d}{2} \]
The relationship between the frictional force and the normal force leads to
\[ F_{Bx}=µ \cdot F_{By} \]
\[ F_{By} = \frac{F_{Bx}}{µ} \]
The moment balances set out below are set up with regard to point A on the operating lever.
Left rotation
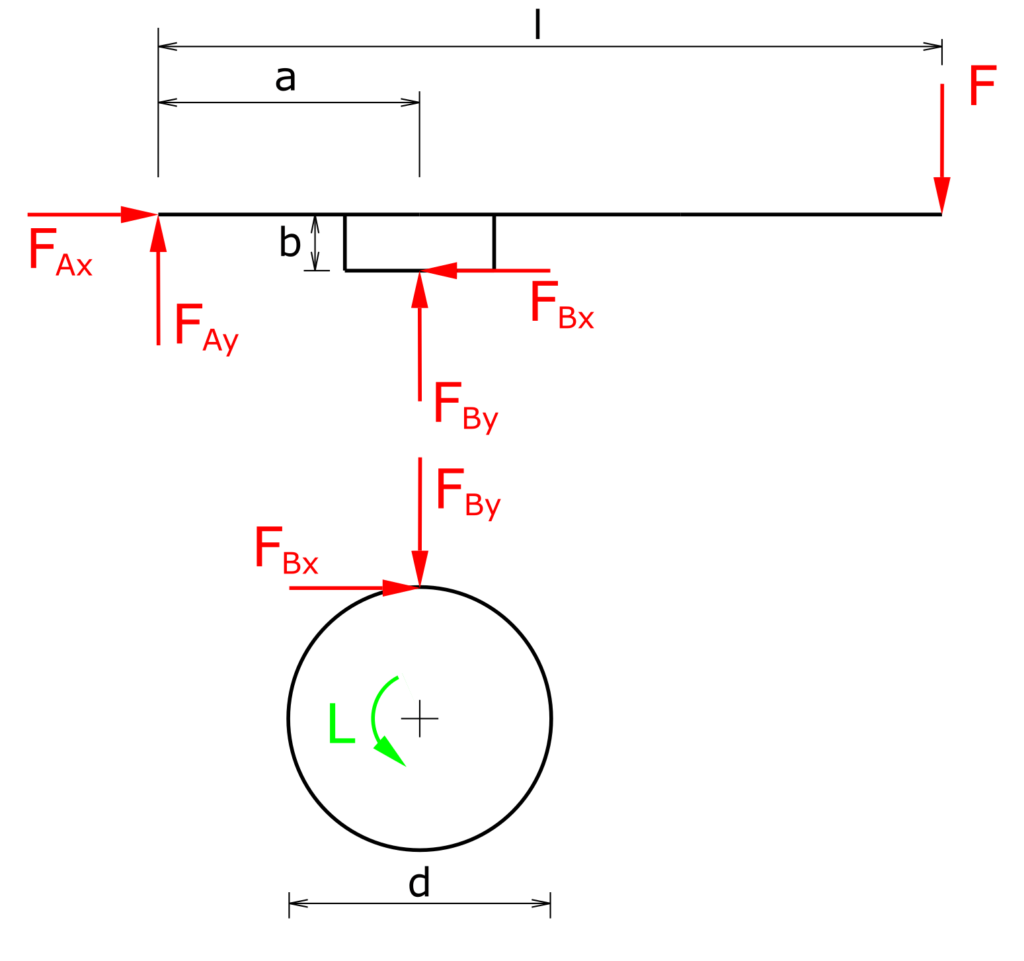
\[ \sum M(A)=0=- F_{Bx} \cdot b + F_{By} \cdot a - F \cdot l \]
\[ 0=-F_{Bx} \cdot b + \frac{F_{Bx}}{µ} \cdot a - F \cdot l \]
\[ F \cdot l=-F_{Bx} \cdot \left( b - \frac{a}{µ} \right) \]
\[ F_{Bx} = - \frac{F \cdot l}{\left( b - \frac{a}{µ} \right)} \]
The braking torque for left turning rotation is
\[ M_{BL}=\frac{F \cdot l \cdot d}{2 \cdot \left( b - \frac{a}{µ} \right)} \]
Right rotation
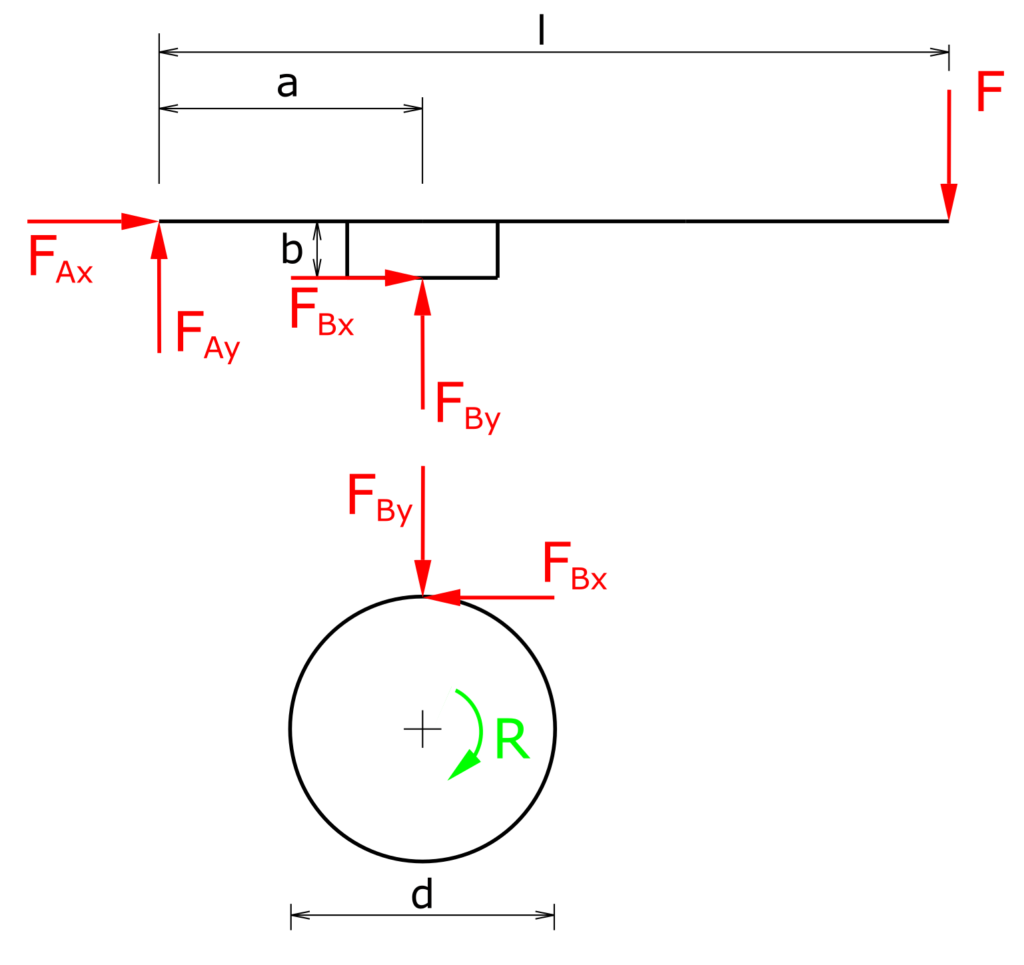
\[ \sum M(A)=0= F_{Bx} \cdot b + F_{By} \cdot a - F \cdot l \]
\[ 0= F_{Bx} \cdot b + \frac{F_{Bx}}{µ} \cdot a - F \cdot l \]
\[ F \cdot l= F_{Bx} \cdot \left( b + \frac{a}{µ} \right) \]
\[ F_{Bx} = \frac{F \cdot l}{\left( b + \frac{a}{µ} \right)} \]
The braking torque for right turning rotation is
\[ M_{BR}= \frac{F \cdot l \cdot d}{2 \cdot \left( b + \frac{a}{µ} \right)} \]
The amount of braking torque in anti-clockwise rotation is higher than in clockwise rotation because the divisor is larger in clockwise rotation. The brake is therefore more effective in anti-clockwise rotation than in clockwise rotation.
Determination of the height b for equally large drum braking torques both rotation directions
The condition is: MBR = -MBL. From this follows
\[ M_{BR} = M_{BL}\]
\[ \frac{F \cdot l \cdot d}{2 \cdot \left( b + \frac{a}{µ} \right)} = -\frac{F \cdot l \cdot d}{2 \cdot \left( b - \frac{a}{µ} \right)}\]
\[ b + \frac{a}{µ} = - b + \frac{a}{µ} \]
\[ b =0 \]
Determination of the height b and direction of rotation for seizing
The brake seizes when the braking torque approaches infinity. This can only occur in counter-clockwise operation when the expression below the fraction line approaches zero.
\[ M_B \rightarrow \infty \]
\[ M_{BL}=\frac{F \cdot l \cdot d}{2 \cdot \left( b - \frac{a}{µ} \right)} \]
\[ b - \frac{a}{µ} = 0 \]
\[ b = \frac{a}{µ} \]
Here we have some more exercises regarding friction in engineering mechanics.

