Werbung
In dieser Übung wird die Biegelinie für einen Kragträger mit ansteigender Dreieckslast berechnet. Wie man die Schnittgrößen für einen Träger mit abfallender Dreieckslast bestimmt, ist hier beschrieben.
Aufgabe
Ein einseitig fest eingespannter Träger wird durch die linear ansteigende Streckenlast (Dreieckslast) q0 belastet. Es ist die Biegelinie für den Träger zu bestimmen!
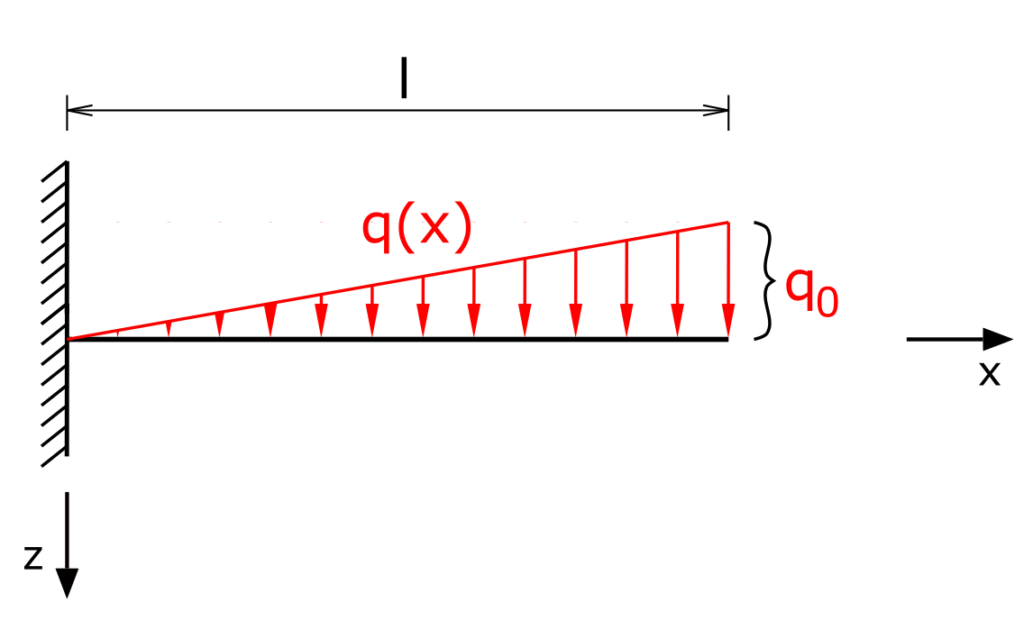
Lösung
Die Dreieckslast muss als Funktion beschrieben werden. Für den vorliegenden Fall lautet sie
\[ \tag{1} q(x) = q_0 \frac{x}{l} \]
Zur Bestimmung der Biegelinie müssen die Schnittgrößen des Trägers ermittelt werden. Dabei ist für die Biegung nur das Biegemoment relevant, d.h. in den folgenden Gleichungen wird nur das Momentengleichgewicht betrachtet.
Es ist in diesem Fall nicht erforderlich, die Lagerreaktionen der festen Einspannung zu ermitteln, da der Schnitt so gewählt wird, dass die Lagerreaktionen entfallen. Die Schnittgrößen können unmittelbar bestimmt werden.
Linksdrehende Momente sind im Folgenden positiv. Die Schnittgrößen werden an einem negativen Schnittufer negativ angetragen. Die Koordinatenrichtung x wird ergänzt um die Hilfskoordinate ξ.
Bestimmung der Schnittgrößen
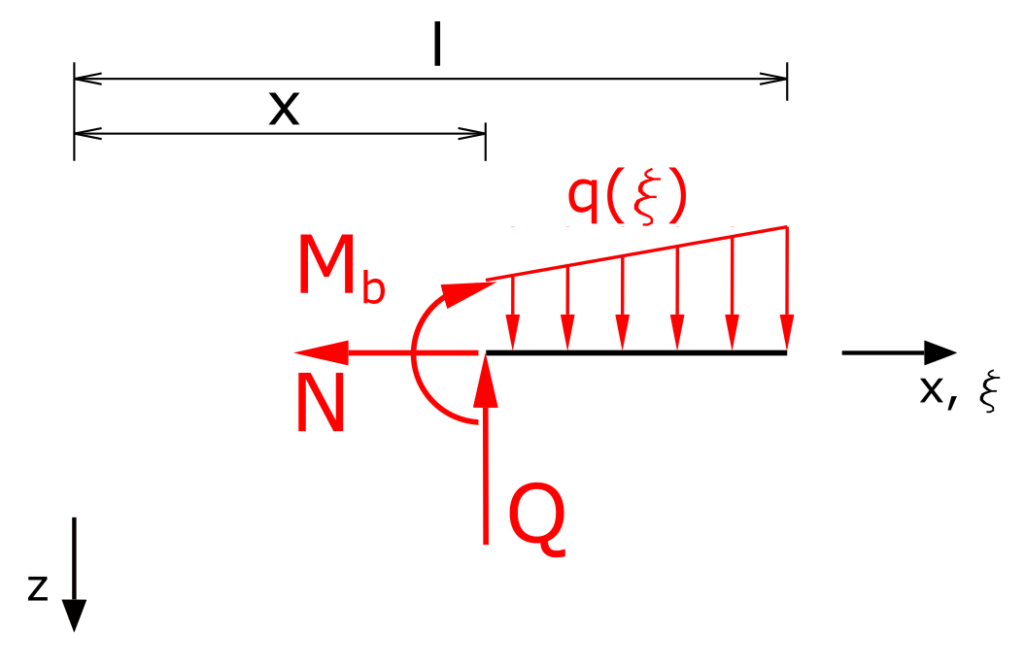
Die Momentenbilanz liefert
\[ \tag{2} \sum M(x) = 0 = -M_b - \int_x^l{q(\xi)\cdot \left( \xi - x \right) d \xi} \]
\[ \tag{3} M_b = - \left( \frac{q_0 x^3 - 3l^2q_0x+2l^3q_0}{6l} \right) \]
Die Biegelinie wird auf Basis der Bernoulli-Balkenbiegung bestimmt. Der grundsätzliche Zusammenhang lautet
\[ w'' = \frac{-M_b}{E \cdot I} \]
Dabei ist w'' die zweite Ableitung der Biegelinie, E der Elastizitätsmodul und I das Flächenträgheitsmoment. Die Biegelinie w erhält man durch zweifache Integration über x. Daraus folgt für den vorliegenden Fall
\[ \tag{4} w'' = \frac{q_0x^3-3l^2q_0x+2l^3q_0}{6EIl} \]
\[ \tag{5} w' = \frac{\frac{q_0x^4}{4}-\frac{3l^2q_0x^2}{2}+2l^3q_0x}{6EIl} + c_1 \]
\[ \tag{6} w = \frac{\frac{q_0x^5}{20}-\frac{l^2q_0x^3}{2}+l^3q_0x^2}{6EIl} +c_1x + c_2 \]
Um die Integrationskonstanten c1 und c2 bestimmen zu können, müssen die Randbedingungen aufgestellt werden.
Randbedingungen
Die erste Bedingung lautet: die Durchbiegung an der Stelle x = 0 ist gleich 0.
\[ \tag{7} w(x=0) = 0 = \frac{\frac{q_00^5}{20}-\frac{l^2q_00^3}{2}+l^3q_00^2}{6EIl} +c_10 + c_2 \]
\[ \tag{8} c_2 = 0\]
Die zweite Bedingung lautet: der Winkel an der Stelle x = 0 ist gleich 0.
\[ \tag{9} w'(x=0) = 0 = \frac{\frac{q_00^4}{4}-\frac{3l^2q_00^2}{2}+2l^3q_00}{6EIl} + c_1 \]
\[ \tag{10} c_1 = 0 \]
Damit ist die Funktion der Biegelinie vollständig definiert. Sie lautet
\[ \tag{11} w = \frac{\frac{q_0x^5}{20}-\frac{l^2q_0x^3}{2}+l^3q_0x^2}{6EIl} \]
Verpasse nicht die anderen Aufgaben in der Kategorie Technische Mechanik II!
Werbung




