In this exercise the bending line is calculated for a cantilever beam with ascending triangular load. How to determine the internal forces for a beam with descending triangular load is described here.
Task
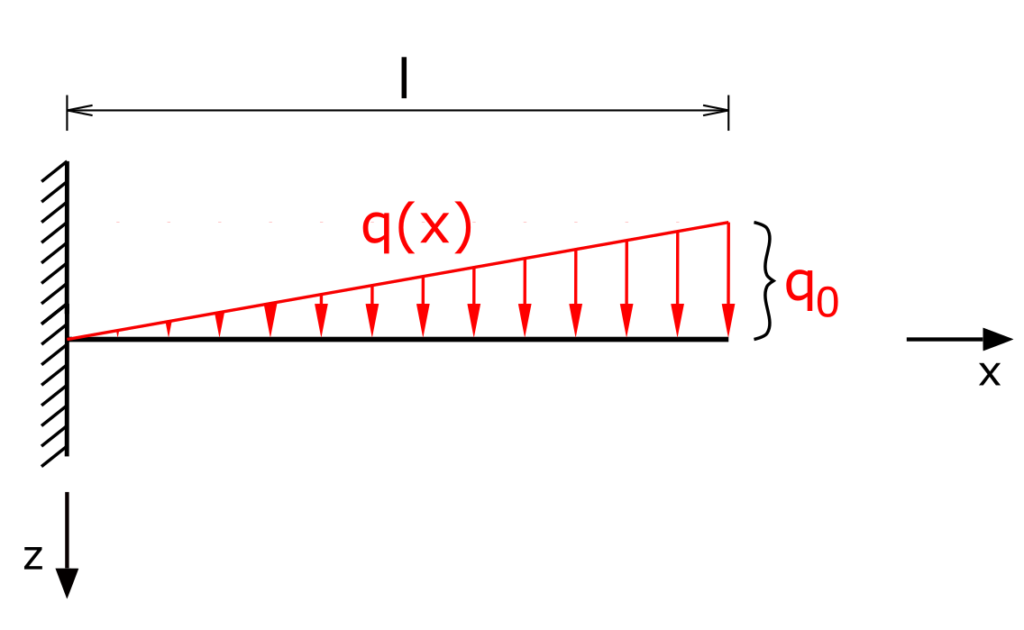
A beam with a fixed restraint on one side is loaded by the linearly increasing line load (triangular load) q0. The bending line for the beam has to be determined!
Solution
The triangular load must be described as a function. In the present case it is
\[ \tag{1} q(x) = q_0 \frac{x}{l} \]
To determine the bending line, the internal forces of the beam must be determined. Only the bending moment is relevant for the bending, i.e. in the following equations only the moment equilibrium is considered.
In this case, it is not necessary to determine the support reactions of the fixed restraint, as the section is chosen in such a way that the support reactions do not occur. The internal forces can be determined directly.
Left-turning moments are positive in the following. The internal forces are applied negatively on a negative cutting edge. The coordinate direction x is supplemented by the auxiliary coordinate ξ.
Determination of the internal forces
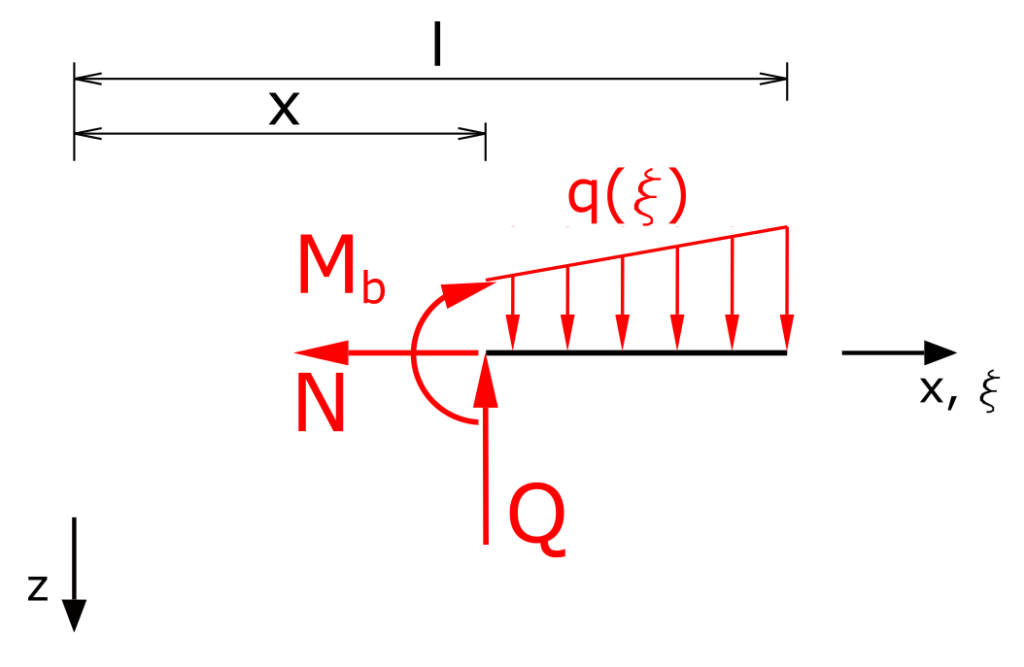
The moment balance delivers
\[ \tag{2} \sum M(x) = 0 = -M_b - \int_x^l{q(\xi)\cdot \left(\xi - x \right) d \xi} \]
\[ \tag{3} M_b = - \left( \frac{q_0 x^3 - 3l^2q_0x+2l^3q_0}{6l} \right) \]
The bending line is determined on the basis of the Bernoulli beam bending. The basic relation is
\[ w'' = \frac{-M_b}{E \cdot I} \]
Here, w'' is the second derivative of the bending line, E is the modulus of elasticity and I is the area moment of inertia. The bending line w is obtained by integrating twice over x. It follows from this for the present case
\[ \tag{4} w'' = \frac{q_0x^3-3l^2q_0x+2l^3q_0}{6EIl} \]
\[ \tag{5} w' = \frac{\frac{q_0x^4}{4}-\frac{3l^2q_0x^2}{2}+2l^3q_0x}{6EIl} + c_1 \]
\[ \tag{6} w = \frac{\frac{q_0x^5}{20}-\frac{l^2q_0x^3}{2}+l^3q_0x^2}{6EIl} +c_1x + c_2 \]
In order to be able to determine the constants of integration c1 and c2, the boundary conditions must be established.
Boundary conditions
The first condition is: the deflection at the point x = 0 is equal to 0.
\[ \tag{7} w(x=0) = 0 = \frac{\frac{q_00^5}{20}-\frac{l^2q_00^3}{2}+l^3q_00^2}{6EIl} +c_10 + c_2 \]
\[ \tag{8} c_2 = 0\]
The second condition is: the angle at the point x = 0 is equal to 0.
\[ \tag{9} w'(x=0) = 0 = \frac{\frac{q_00^4}{4}-\frac{3l^2q_00^2}{2}+2l^3q_00}{6EIl} + c_1 \]
\[ \tag{10} c_1 = 0 \]
The bending line for the cantilever beam with ascending triangular load is thus completely defined. It is
\[ \tag{11} w = \frac{\frac{q_0x^5}{20}-\frac{l^2q_0x^3}{2}+l^3q_0x^2}{6EIl} \]
Don't miss the other exercises regarding Engineering Mechanics II!

