Werbung
Aufgabe
Die Kraft F greift in der dargestellten Weise an einem Gelenkträger an. Bestimmen Sie die Reaktionskräfte in A, B und C.
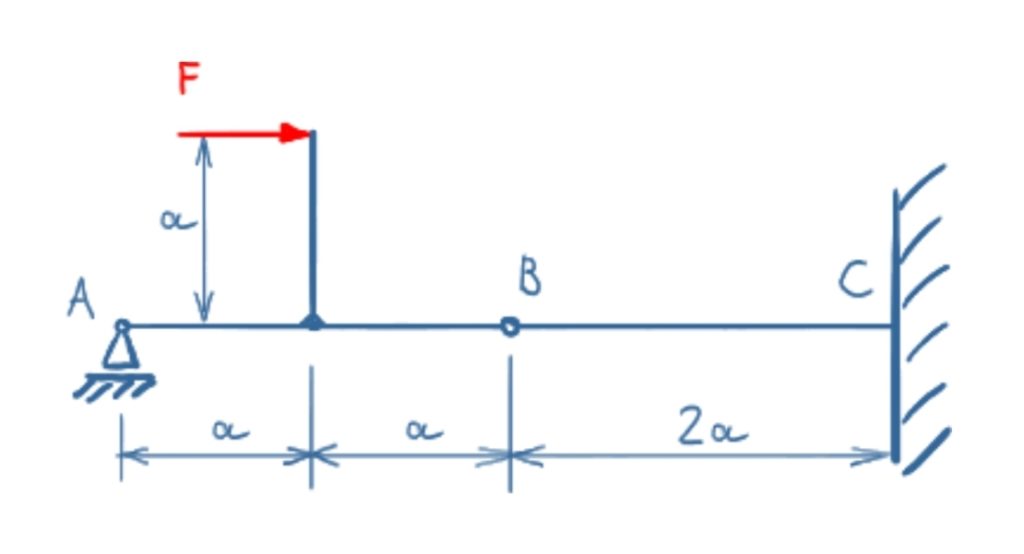
Lösung
Der Träger wird zur Ermittlung der Lagerreaktionen und Gelenkkräfte in zwei Bereiche eingeteilt.
Bereich 1
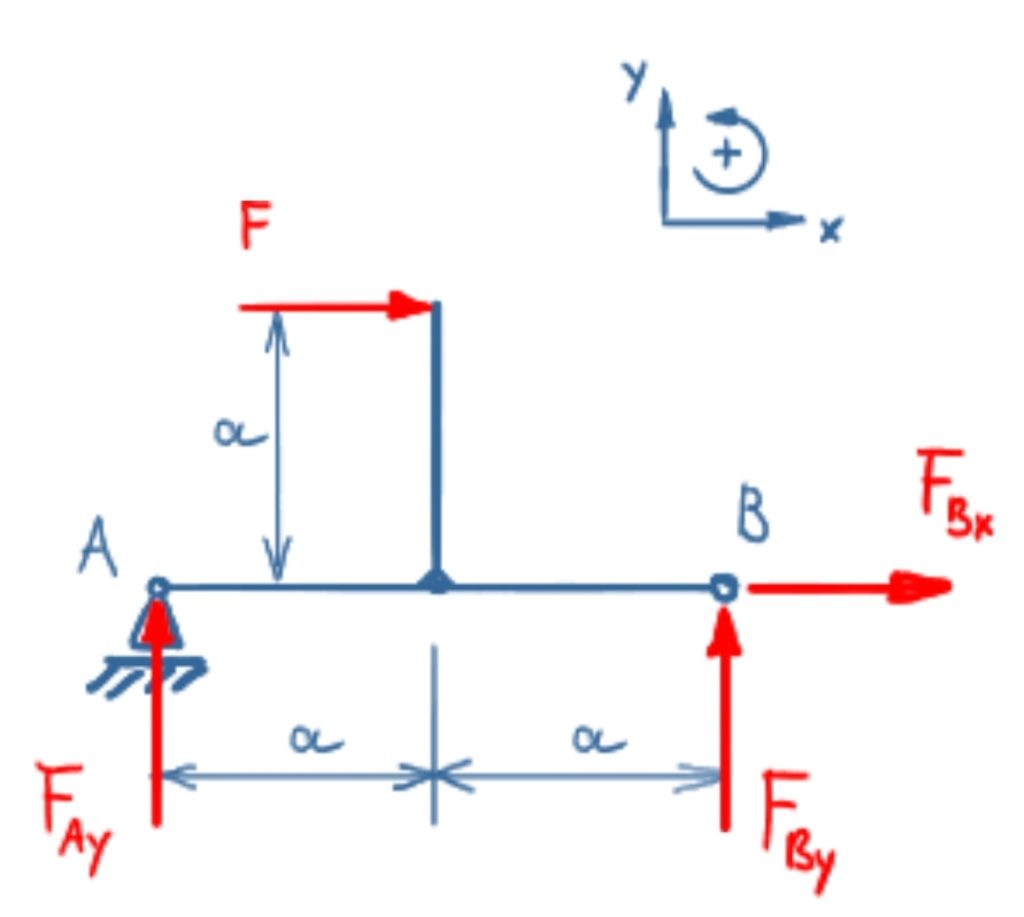
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{1} \sum F_x = 0 = F + F_{Bx} \]
\[\tag{2} F_{Bx} = -F \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{3} \sum F_y = 0 = F_{Ay} + F_{By} \]
Das Momentengleichgewicht um Punkt A ergibt
\[\tag{4} \sum M(A) = 0 = -F \cdot a + F_{By} \cdot 2 \cdot a \]
\[\tag{5} F_{By} = \frac{F \cdot \bcancel{a}}{2 \cdot \bcancel{a}} \]
Damit ergibt sich aus Gleichung 3
\[\tag{6} F_{Ay} = - \frac{F}{2} \]
Bereich 2:
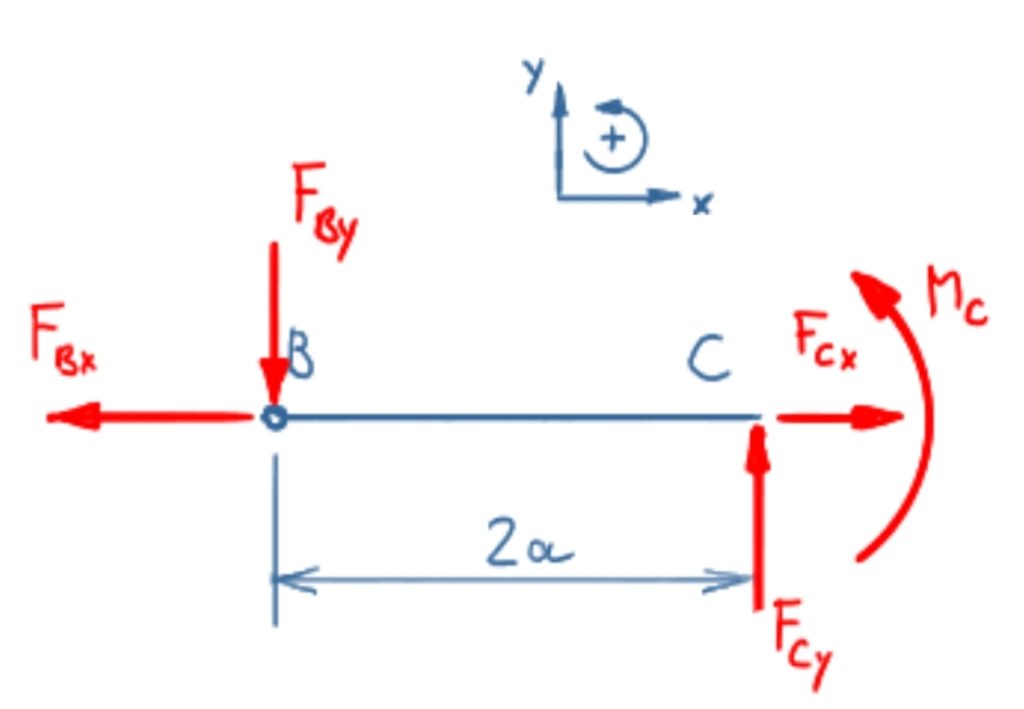
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{7} \sum F_x = 0 = - F_{Bx} + F_{Cx} \]
\[\tag{8} F_{Cx} = -F \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{9} \sum F_y = 0 = - F_{By} + F_{Cy} \]
\[\tag{10} F_{Cy} = \frac{F}{2} \]
Das Momentengleichgewicht um Punkt C ergibt
\[\tag{11} \sum M(C) = 0 = F_{By} \cdot 2a + M_C \]
\[\tag{12} M_C = - F \cdot a \]
Werbung




