Werbung
In dieser Übung werden folgende Fragen behandelt:
- Wie ermittle ich Kraft und Richtung einer fehlenden Größe, wenn die resultierende Kraft vorgegeben ist?
- Wie löst man zwei Gleichungen mit zwei Unbekannten (bzw. ein einfaches Gleichungssystem)?
- Wie bestimme ich den Winkel einer Kraft?
Aufgabe
Ein Schiff wird von drei Schleppern gezogen. Schlepper 1 zieht mit F1 = 7 kN, Schlepper 2 mit F2 = 6 kN. Für Schlepper 3 wird sowohl die Kraft als auch der Winkel für den Fall gesucht, dass die resultierende Kraft 10 kN in x-Richtung beträgt.
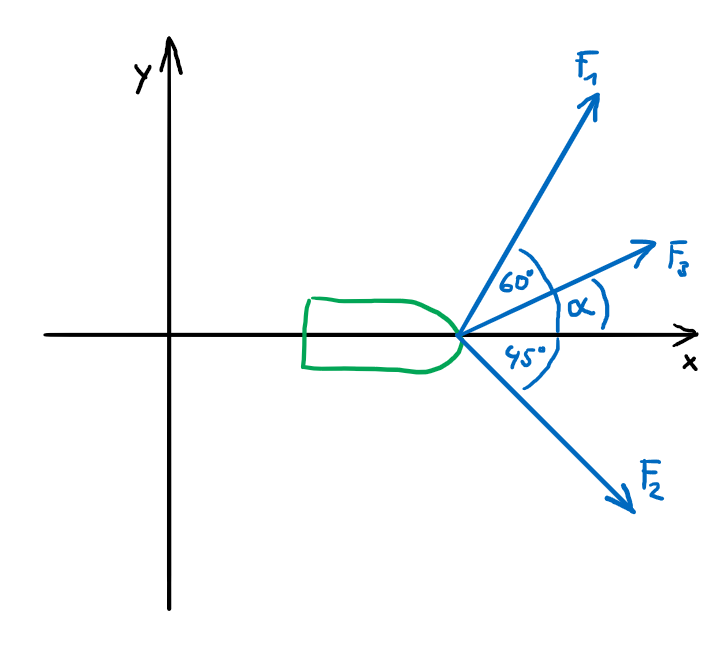
Lösung
Die Randbedingungen zur Lösung lauten: die Summe aller Kräfte in x-Richtung beträgt 10 kN, die Summe aller Kräfte in y-Richtung beträgt Null. Der Winkel von F3 wird hierbei erst einmal so wie in der Skizze angenommen.
\[\tag{1} \sum F_x= 10 kN = F_1\cos(60°)+F_2\cos(45°)+F_3\cos(\alpha)\]
\[\tag{2} \sum F_y= 0 = F_1\sin(60°)-F_2\sin(45°)+F_3\sin(\alpha)\]
Gleichung 1 wird nach F3 aufgelöst und in Gleichung 2 eingesetzt.
\[\tag{3} F_3= \frac{10 kN - F_1\cos(60°) - F_2\cos(45°)}{\cos(\alpha)}\]
\[\tag{4} 0 = F_1\sin(60°)-F_2\sin(45°)+\frac{10 kN - F_1\cos(60°) - F_2\cos(45°)}{\cos(\alpha)}\sin(\alpha) \]
Gleichung 4 wird aufgelöst nach
\[\tag{5} \alpha = \arctan\left(\frac{F_2\sin(45°)-F_1\sin(60°)}{10 kN - F_1\cos(60°) - F_2\cos(45°)}\right) \]
\[\tag{6} \alpha = -38.87° \]
und die gesuchte Kraft ergibt sich zu
\[\tag{7} F_3 = 2.9 kN \]
Damit sind Kraft und Winkel bestimmt, um die gewünschte resultierende Zugrichtung zu erreichen. Es zeigt sich, dass der Winkel für Schlepper 3 auf der gegenüberliegenden Seite der x-Achse liegen muss. Die getroffene Annahme für den Winkel ist also falsch, was aber die Berechnung nicht beeinträchtigt.
Hätte man den Winkel gleich unterhalb der x-Achse angetragen, hätte man einen positiven Wert für den Winkel erhalten.
Hier gibt es weitere Aufgaben zum Thema resultierende Kräfte.
Werbung




