Werbung
Aufgabe
Ein Gewicht G zieht unter dem Winkel α symmetrisch an zwei Gleitschlitten. Wie groß muss die Haftreibung mindestens sein, damit Gleichgewicht herrscht? Die Abmessungen der Gleitschlitten können hierbei vernachlässigt werden.
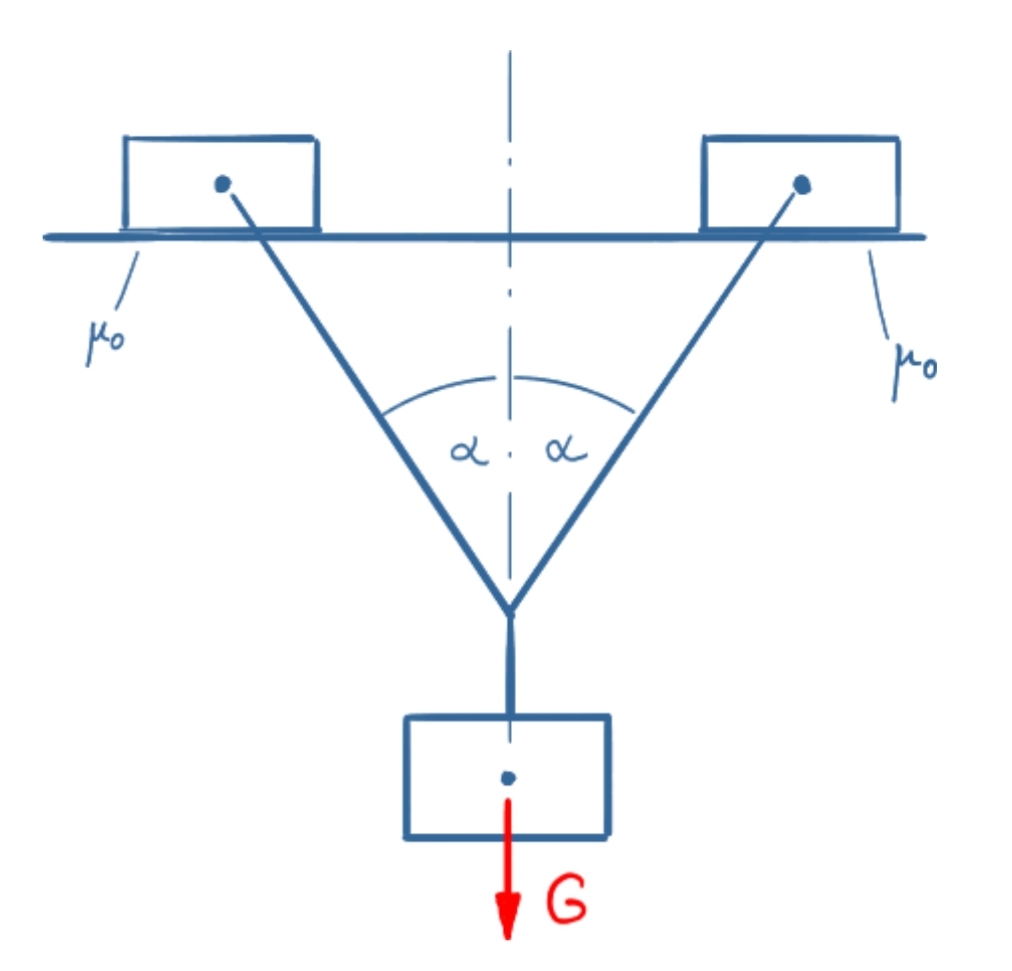
Lösung
Nachfolgend ein Video, in dem diese Aufgabe vorgerechnet wird:
Und hier der Lösungsweg zum Nachlesen:
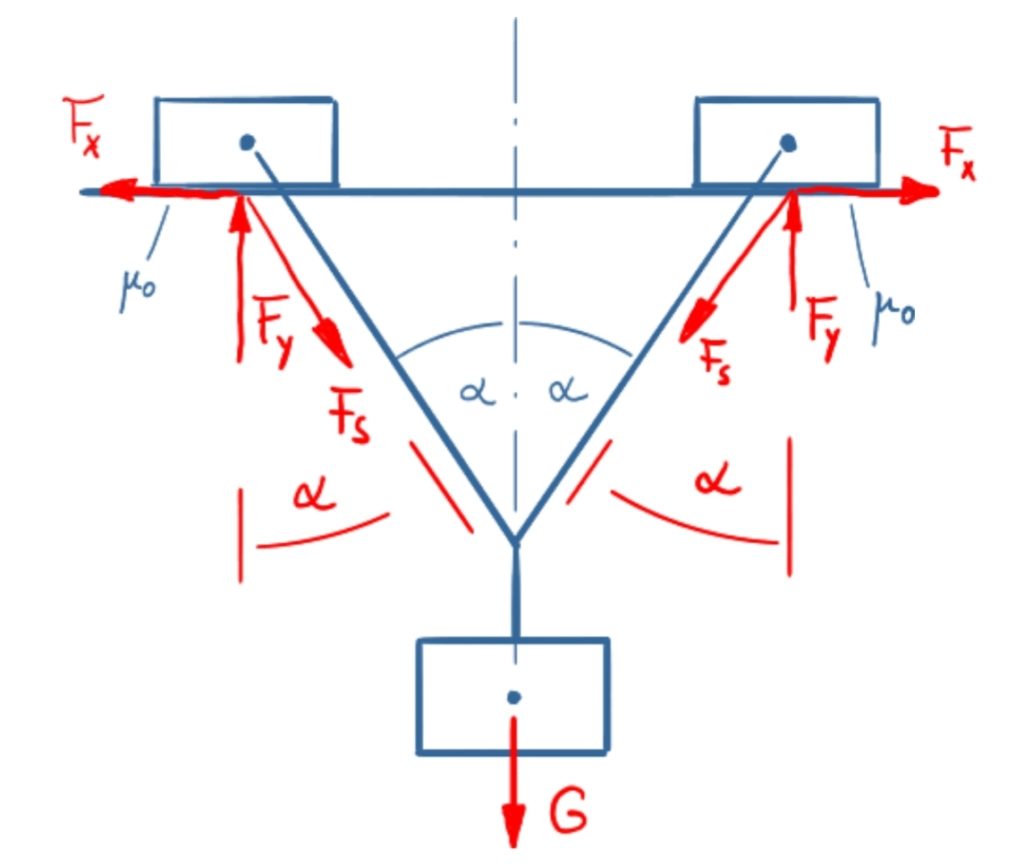
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
\[\tag{1} 0={F_S} \sin{\left( \alpha \right) }-{F_x}\]
\[\tag{2} 0={F_y}-{F_S} \cos{\left( \alpha \right) }\]
\[\tag{3} {F_x}={F_y} {µ_0}\]
\[\tag{4} {F_S} \cos{\left( \alpha \right) }=\frac{G}{2}\]
\[\tag{5} {F_S}=\frac{G}{2 \cos{\left( \alpha \right) }}\]
\[\tag{6} 0=\frac{G \sin{\left( \alpha \right) }}{2 \cos{\left( \alpha \right) }}-{F_x}\]
\[\tag{7} {F_x}=\frac{G \sin{\left( \alpha \right) }}{2 \cos{\left( \alpha \right) }}\]
\[\tag{8} {F_y}={F_S} \cos{\left( \alpha \right) }\]
\[\tag{9} {F_y}=\frac{G}{2}\]
\[\tag{10} {µ_0}=\frac{{F_x}}{{F_y}}\]
\[\tag{11} {µ_0}=\frac{2 {F_x}}{G}\]
\[\tag{12} {µ_0}=\frac{\sin{\left( \alpha \right) }}{\cos{\left( \alpha \right) }}\]
\[\tag{13} {µ_0}=\tan{\left( \alpha \right) }\]
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Reibung.
Werbung





die Höhe der Gleitklötze wird vernachlässigt