Werbung
In dieser Übung wird gezeigt, wie der Schwerpunkt zusammengesetzter Körper berechnet wird.
Aufgabe
Für den abgebildeten Körper soll der Schwerpunkt berechnet werden. Der Körper besteht aus zwei Einzelkörpern unterschiedlichen Materials.
Gegeben:
a = 30 mm, b = 25 mm, c = 60 mm, d = 30 mm, e = 50 mm
Körper 1 besteht aus Stahl mit einer Dichte von ρ = 7.850 kg/m³,
Körper 2 besteht aus Aluminium mit einer Dichte von ρ = 2.660 kg/m³.
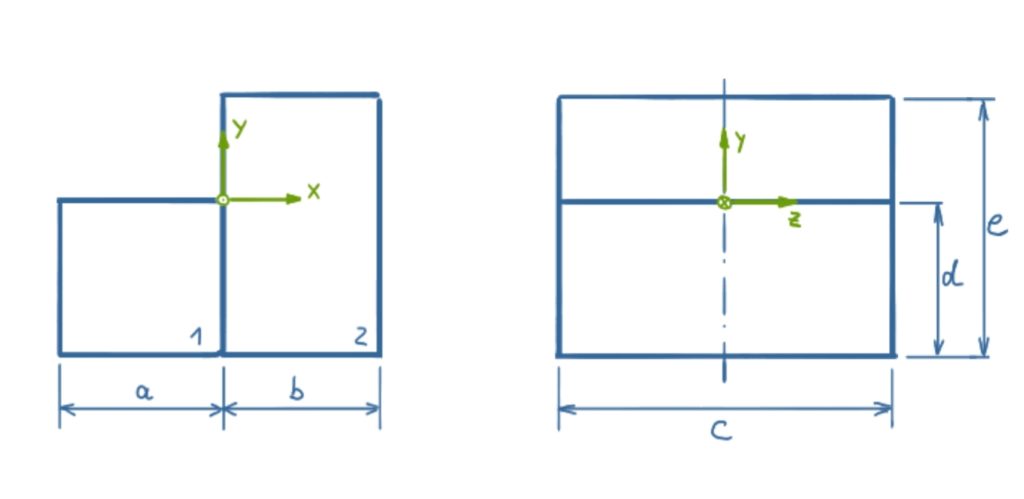
Ein Hinweis zur Projektionsrichtung: ein Kreis mit einem Mittelpunkt kennzeichnet eine Koordinatenachse, die auf den Betrachter zeigt. Ein Kreis mit einem Kreuz ist eine Koordinatenachse, die vom Betrachter weg zeigt.
Lösung
\[ \require{cancel} \]Die Gleichung zur Berechnung der Schwerpunktkoordinate lautet, hier exemplarisch für xS notiert:
\[ \tag{1} x_S = \frac{\sum \rho_i \cdot V_i \cdot x_i}{\sum \rho_i \cdot V_i} \]
Die Werte der Einzelkörper werden in einer Tabelle erfasst
| \[ i \] | \[ V_i \] | \[ x_i \] | \[ y_i \] | \[ z_i \] | \[ \rho_i \] | \[ \rho_i \cdot V_i \] | \[ \rho_i \cdot V_i \cdot x_i \] | \[ \rho_i \cdot V_i \cdot y_i \] | \[ \rho_i \cdot V_i \cdot z_i \] |
|---|---|---|---|---|---|---|---|---|---|
| \[ {mm}^3 \] | \[ mm \] | \[ mm \] | \[ mm \] | \[ 10^{-6}kg/{mm}^3 \] | \[ kg \] | \[ kgmm \] | \[ kgmm \] | \[ kgmm \] | |
| 1 | 54.000 | -15 | -15 | 0 | 7,85 | 0,424 | -6,359 | -6,359 | 0 |
| 2 | 75.000 | 12,5 | -5 | 0 | 2,66 | 0,2 | 2,494 | -0,998 | 0 |
| \[ \sum \] | 0,624 | -3,865 | -7,357 | 0 |
Damit ergeben sich folgende Schwerpunktkoordinaten:
\[ \tag{2} x_S = \frac{-3.865 kg\,mm}{0.624kg} = -6.2\,mm \]
\[ \tag{3} y_S = \frac{-7.357 kg\,mm}{0.624kg} = -11.8\,mm \]
\[ \tag{4} z_S = \frac{0 kg\,mm}{0.624kg} = 0\,mm \]
Damit ist der Schwerpunkt des zusammengesetzten Körpers bestimmt.
Weitere Aufgaben zum Thema Schwerpunkt gibt es unter dem Schlagwort Schwerpunkt.
Werbung




