Werbung
Diese Übung beschäftigt sich mit der Kippstabilität eines geschobenen Körpers und behandelt folgende Fragen:
- Wie berechnet man die Kippstabilität eines geschobenen Körpers, wenn die Reibung mit berücksichtigt werden muss?
- Welche Reaktionskräfte treten an einem geschobenen Körper auf?
Aufgabe
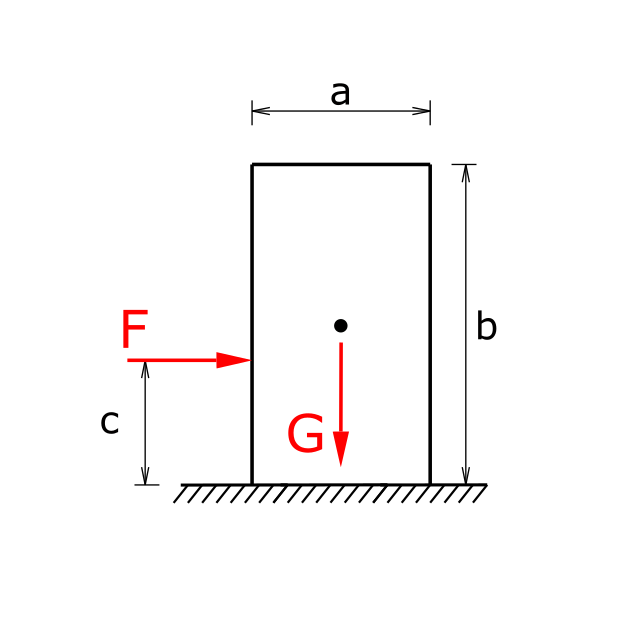
Ein Körper soll auf einer Gleitfläche mit der Kraft F aus dem Ruhezustand verschoben werden. Wie groß darf der Haftreibungskoeffizient µ0 höchstens sein, damit der Körper nicht kippt?
Lösung
Die Reaktionskräfte werden in einer Skizze angetragen.
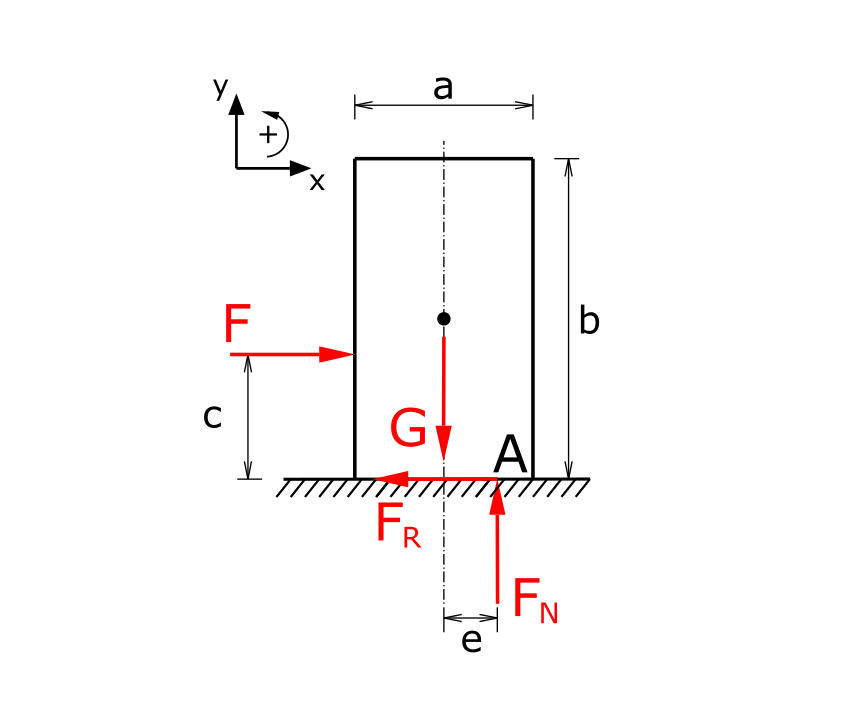
Die Reaktionskräfte sind die Normalkraft FN und die Reibkraft FR. Der Angriffspunkt der Normalkraft ist hierbei um den Abstand e verschoben. Die Kante, um die der Körper kippen würde, wird mit A bezeichnet.
Die Kräfte- und Momentengleichgewichte (linksdrehende Momente positiv) lauten:
\[ \tag{1} \sum F_x = 0 = F - F_R \]
\[ \tag{2} \sum F_y = 0 = - G + F_N \]
\[ \tag{3} \sum M(A) = 0 = - F \cdot c + G \cdot \frac{a}{2} - F_N \cdot \left( \frac{a}{2}-e \right) \]
Der Zusammenhang zwischen Reibkraft und Normalkraft lautet für den Moment des Losreißens
\[ \tag{4} F_R = µ_0 \cdot F_N \]
Aus den ersten beiden Gleichungen folgen
\[ \tag{5} F_R = F \]
\[ \tag{6} F_N = G \]
Damit wird aus Gleichung (5)
\[ \tag{7} F = µ_0 \cdot G \]
Gleichung (3) kann so umgestellt und nach e aufgelöst werden zu
\[ \tag{8} 0 = - µ_0 \cdot G \cdot c + G \cdot \frac{a}{2} - G \cdot \left( \frac{a}{2}-e \right) \]
\[ \tag{9} e = c \cdot µ_0 \]
Der Körper kippt, wenn der Abstand e größer wird als a/2. Also lautet die Bedingung für den stabilen Stand
\[ \tag{10} e \leq \frac{a}{2} \]
\[ \tag{11} c \cdot µ_0 \leq \frac{a}{2} \]
Der Haftreibungskoeffizient muss also folgende Größe annehmen
\[ \tag{12} µ_0 \leq \frac{a}{2 \cdot c} \]
Hier gibt es weitere interessante Übungsaufgaben zum Thema Reibung.
Diese Seite bietet weitere Übersichtstabellen mit Reibungskoeffizienten.
Werbung




