This exercise investigates the tipping stability of a pushed body taking static friction into account.
Task
A body is supposed to be moved out of its resting state on a sliding surface with the force F. How large can the coefficient of static friction µ0 be at most so that the body does not tip over?
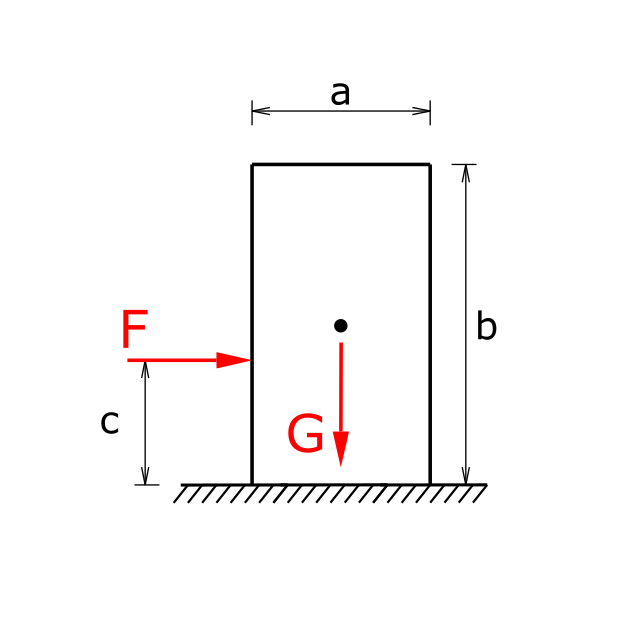
Solution
The reaction forces are plotted in a sketch.
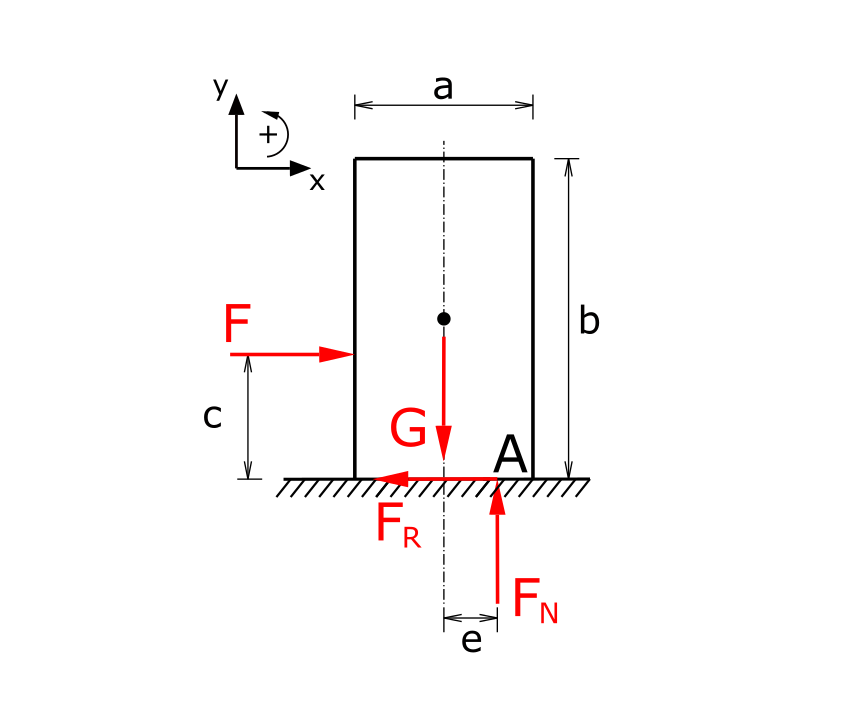
The reaction forces are the normal force FN and the frictional force FR. The point of application of the normal force is shifted by the distance e. The edge around which the body would tip is denoted by A.
The equilibria of forces and moments (counterclockwise moments are positive) are:
\[ \tag{1} \sum F_x = 0 = F - F_R \]
\[ \tag{2} \sum F_y = 0 = - G + F_N \]
\[ \tag{3} \sum M(A) = 0 = - F \cdot c + G \cdot \frac{a}{2} - F_N \cdot \left( \frac{a}{2}-e \right) \]
The relationship between frictional force and normal force is for the moment of tearing away
\[ \tag{4} F_R = µ_0 \cdot F_N \]
It follows from the first two equations
\[ \tag{5} F_R = F \]
\[ \tag{6} F_N = G \]
And equation (5) becomes
\[ \tag{7} F = µ_0 \cdot G \]
Equation (3) can be rearranged and solved for e to
\[ \tag{8} 0 = - µ_0 \cdot G \cdot c + G \cdot \frac{a}{2} - G \cdot \left( \frac{a}{2}-e \right) \]
\[ \tag{9} e = c \cdot µ_0 \]
The body tilts when the distance e is greater than a / 2. So the condition for stability is
\[ \tag{10} e \leq \frac{a}{2} \]
\[ \tag{11} c \cdot µ_0 \leq \frac{a}{2} \]
The coefficient of static friction must therefore assume the following value
\[ \tag{12} µ_0 \leq \frac{a}{2 \cdot c} \]
This exercise is part of the collection Engineering Mechanics I.

