Werbung
In dieser Übung wird ein resultierendes Moment bei schräg angreifender Kraft bzw. mehreren Kräften mit unterschiedlichen Winkeln berechnet.
Aufgabe
Welches Moment erzeugen die Kräfte F1, F2 und F3 bezüglich Punkt P?
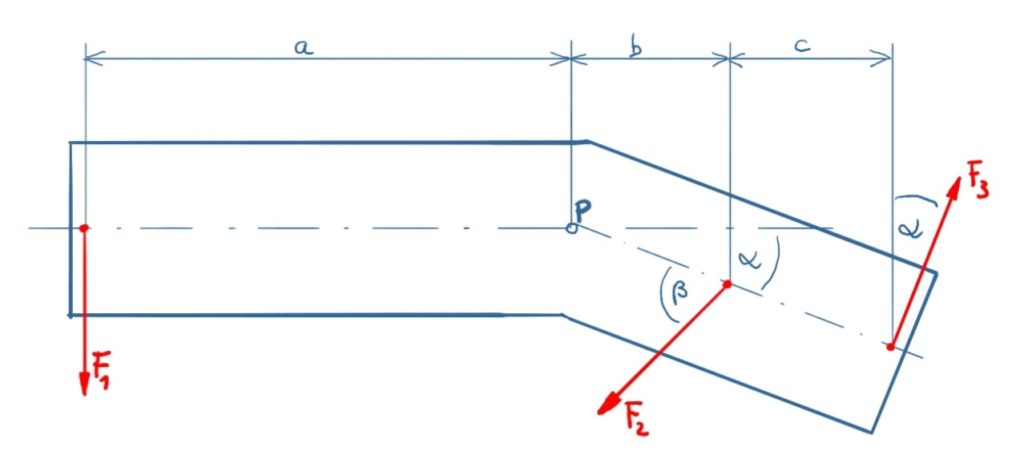
Lösung
Lösungsskizze
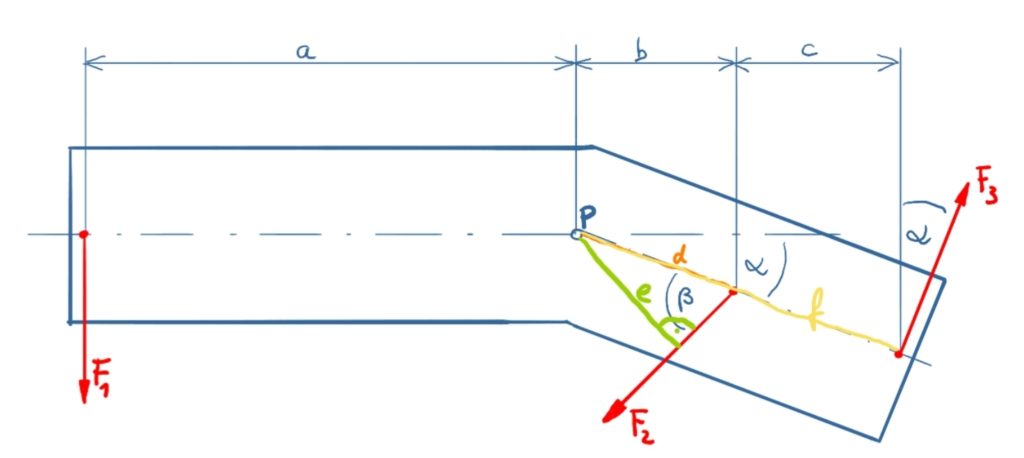
Lösungsweg
In der nachfolgenden Lösung werden linksdrehende Momente als positiv festgelegt. In der Lösungsskizze sind die Hebelarme zu den Kräften F2 in grün (Strecke e) und F3 in hell-orange (Strecke f) bezeichnet.
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]Das resultierende Moment in P beträgt
\[\tag{1} M_P = F_1 \cdot a - F_2 \cdot e + F_3 \cdot f \]
Der Hebelarm e lässt sich wie folgt berechnen:
\[\tag{2} e = d \cdot \sin \beta \]
Die Strecke d ergibt sich aus
\[\tag{3} d = \frac{b}{\cos \alpha} \]
In Gleichung 2 eingesetzt ergibt dies
\[\tag{4} e = \frac{b}{\cos \alpha} \cdot \sin \beta \]
Die Strecke f ergibt sich aus
\[\tag{5} f = \frac{b+c}{\cos \alpha} \]
Das resultierende Moment im Punkt P beträgt damit
\[\tag{6} M_P = F_1 \cdot a - F_2 \cdot \frac{b}{\cos \alpha} \cdot \sin \beta + F_3 \cdot \frac{b+c}{\cos \alpha} \]
Werbung




