Werbung
Diese Übung ist Bestandteil der Aufgabensammlung Technische Mechanik II; es wird eine ebener Spannungszustand untersucht.
Aufgabe
Folgender Spannungszustand ist gegeben:
\[ \newcommand{\myvec}[1]{{\begin{bmatrix}#1\end{bmatrix}}} \]\[ S = \myvec{2 & 1 & 0\\1 & 1 & 0\\0 & 0 & 0} \cdot 100 \, Nmm^{-2} \]
Handelt es sich um einen einachsigen, ebenen oder räumlichen Spannungszustand? Ermitteln Sie die Hauptspannungen und deren Richtungen!
Lösung
Ein einachsiger Spannungszustand liegt vor, wenn nur σx oder σy oder σz gegeben ist (eine Übungsaufgabe für den einachsigen Spannungszustand gibt es hier). Ein ebener Spannungszustand kann zwei Hauptspannungen und eine Schubspannung aufweisen. Dies ist hier der Fall, es handelt sich also um einen ebenen Spannungszustand.
Die Hauptspannungen σ1 und σ2 und der Winkel φ0 lassen sich mit dem Mohr'schen Spannungskreis ermitteln, was zu folgender Darstellung führt:
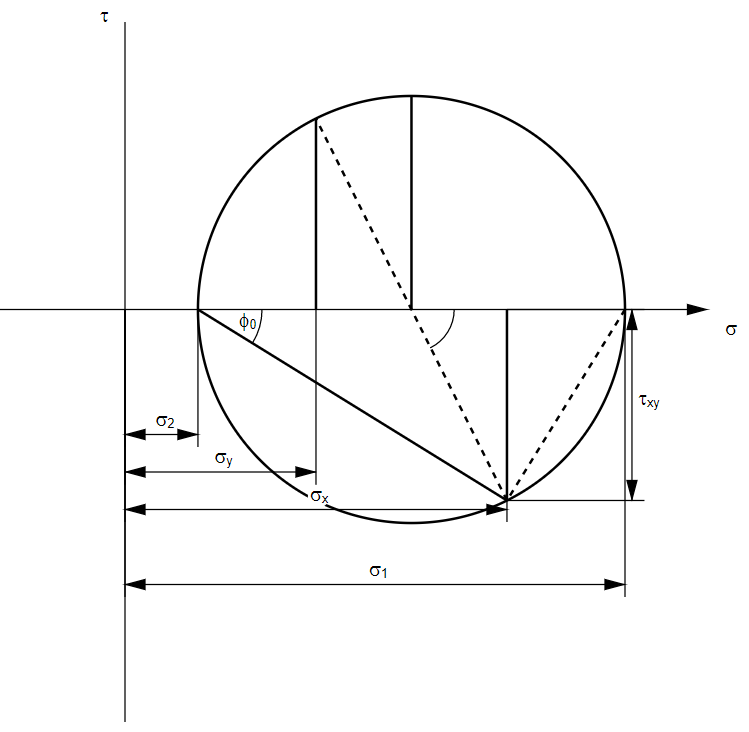
Wenn die Spannungen σx, σy und τxy maßstäblich abgetragen werden, lassen sich die Hauptspannungen und der Winkel aus dem Mohr'schen Spannungskreis abmessen.
Alternativ dazu können die Werte wie folgt berechnet werden.
\[ \tag{1} \sigma_{1,2} = \frac{\sigma_x+\sigma_y}{2} \pm \sqrt{\left( \frac{\sigma_x -\sigma_y}{2}\right)^2 + \tau_{xy}^2} \]
\[ \tag{2} \sigma_{1} = 262\,Nmm^{-2} \]
\[ \tag{3} \sigma_{2} = 38\,Nmm^{-2} \]
Für den Winkel φ0 gilt
\[ \tag{4} tan2\phi_0 = \frac{2 \tau_{xy}}{\sigma_x - \sigma_y} \]
\[ \tag{5} \phi_0 = \frac{1}{2} \cdot arctan \left( \frac{2 \tau_{xy}}{\sigma_x - \sigma_y} \right) \]
\[ \tag{6} \phi_0 = 31.7° \]
Es handelt sich bei φ0 um die Richtung der Hauptspannung σ1. Die Richtung für σ2 ist φ0 + π/2. Damit sind die Hauptspannungen und ihre Richtungen für den hier vorliegenden ebenen Spannungszustands bestimmt.
Werbung




