Task
The following stress state is given:
\[ \newcommand{\myvec}[1]{{\begin{bmatrix}#1\end{bmatrix}}} \]\[ S = \myvec{2 & 1 & 0\\1 & 1 & 0\\0 & 0 & 0} \cdot 100 \, Nmm^{-2} \]
Is it an uniaxial, plane or spatial stress state? Determine the principal stresses and their directions!
Solution
An uniaxial stress state exists if only σx or σy or σz is given (an exercise for the uniaxial stress state is available here). A plane stress state can have two principal stresses and one shear stress. This is the case here, so it is a plane stress state.
The principal stresses σ1 and σ2 and the angle φ0 can be determined with Mohr's circle of stress, which leads to the following representation:
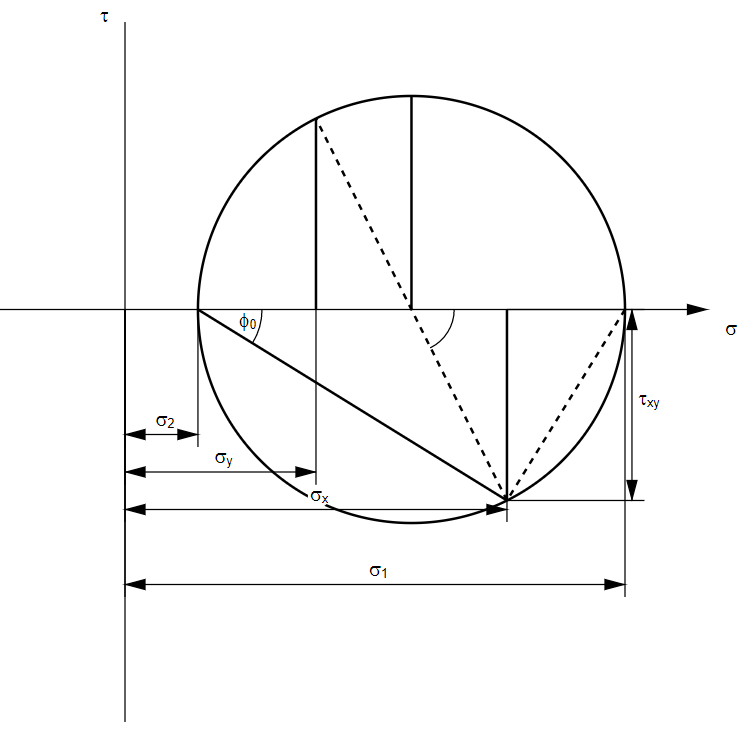
If the stresses σx, σy and τxy are plotted to scale, the principal stresses and the angle can be measured from Mohr's circle of stresses.
Alternatively, the values can be calculated as follows.
\[ \tag{1} \sigma_{1,2} = \frac{\sigma_x+\sigma_y}{2} \pm \sqrt{\left( \frac{\sigma_x -\sigma_y}{2}\right)^2 + \tau_{xy}^2} \]
\[ \tag{2} \sigma_{1} = 262\,Nmm^{-2} \]
\[ \tag{3} \sigma_{2} = 38\,Nmm^{-2} \]
For the angle φ 0 applies
\[ \tag{4} tan2\phi_0 = \frac{2 \tau_{xy}}{\sigma_x - \sigma_y} \]
\[ \tag{5} \phi_0 = \frac{1}{2} \cdot arctan \left( \frac{2 \tau_{xy}}{\sigma_x - \sigma_y} \right) \]
\[ \tag{6} \phi_0 = 31.7° \]
φ0 is the direction of the principal stress σ1. The direction for σ2 is φ0 + π / 2. The principal stresses and their directions are thus determined for the plane stress state present here.

