Werbung
Diese Übung beschäftigt sich mit den Schnittgrößen eines abgewinkelten Trägers und behandelt folgende Fragen:
- Wie ermittelt man die Beanspruchungsgrößen eines Trägers?
- Wie teilt man einen Träger in verschiedene Bereiche ein?
- Wie stellt man die Schnittkräfte grafisch dar?
- Wie stellt man den Verlauf des Biegemoments grafisch dar?
Aufgabe
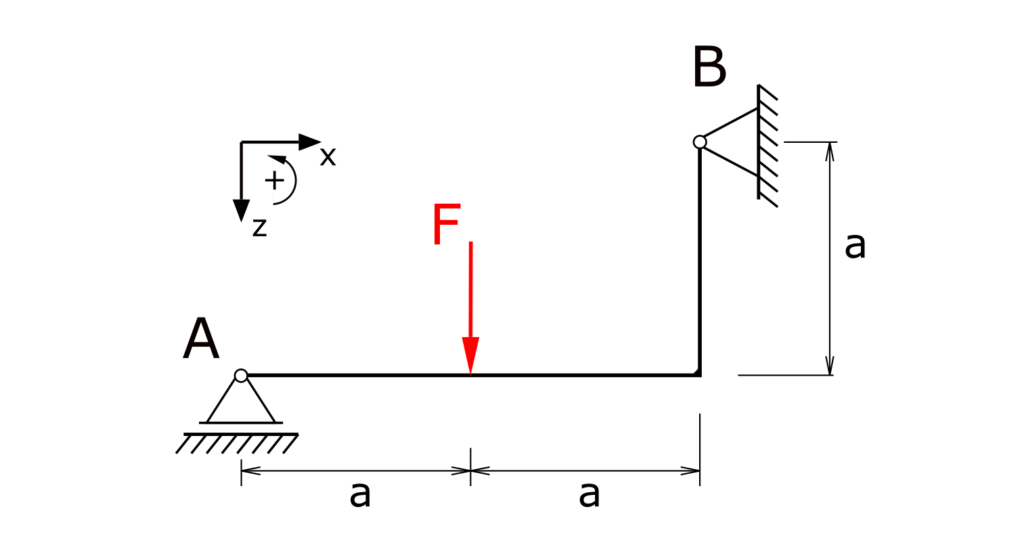
Ein abgewinkelter Träger mit Festlager und Loslager wird durch die Kraft F belastet. Zu ermitteln sind die inneren Kräfte (Schnittgrößen) des Trägers!
Lösung
Zur Berechnung der inneren Kräfte des Trägers werden die Lagerreaktionen ermittelt und der Träger wird in drei Bereiche eingeteilt. Die Querkräfte werden im Folgenden mit Q bezeichnet, die Normalkräfte mit N und das Biegemoment mit Mb. Linksdrehende Momente sind positiv.
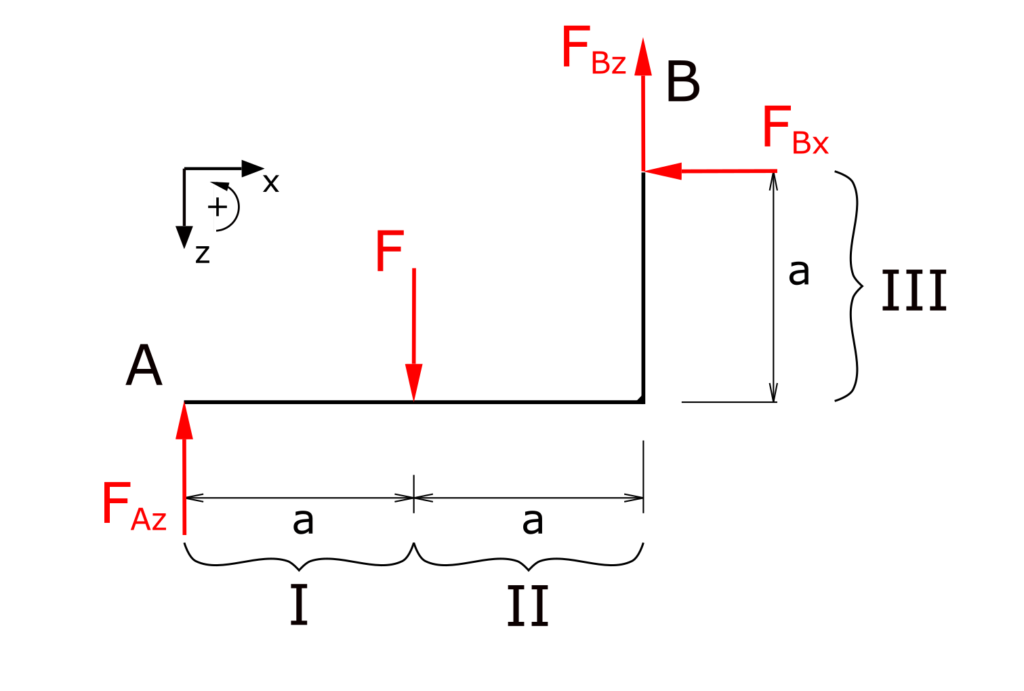
Ermittlung der Lagerreaktionen
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x-und z-Richtung sowie für die Momente
Zu beachten ist die abwärts gerichtete z-Achse!
\[ \tag{1} \sum F_x = 0 = -F_{Bx} \]
\[ \tag{2} \sum F_z = 0 = - F_{Az} + F - F_{Bz} \]
\[ \tag{3} \sum M(A) = 0 = - F \cdot a + F_{Bz} \cdot 2a + F_{Bx} \cdot a \]
Daraus folgt
\[ \tag{4} F_{Bx} = 0 \]
\[ \tag{5} F_{Bz} = \frac{F}{2} \]
\[ \tag{6} F_{Az} = \frac{F}{2} \]
Ermittlung der Schnittgrößen in Bereich I
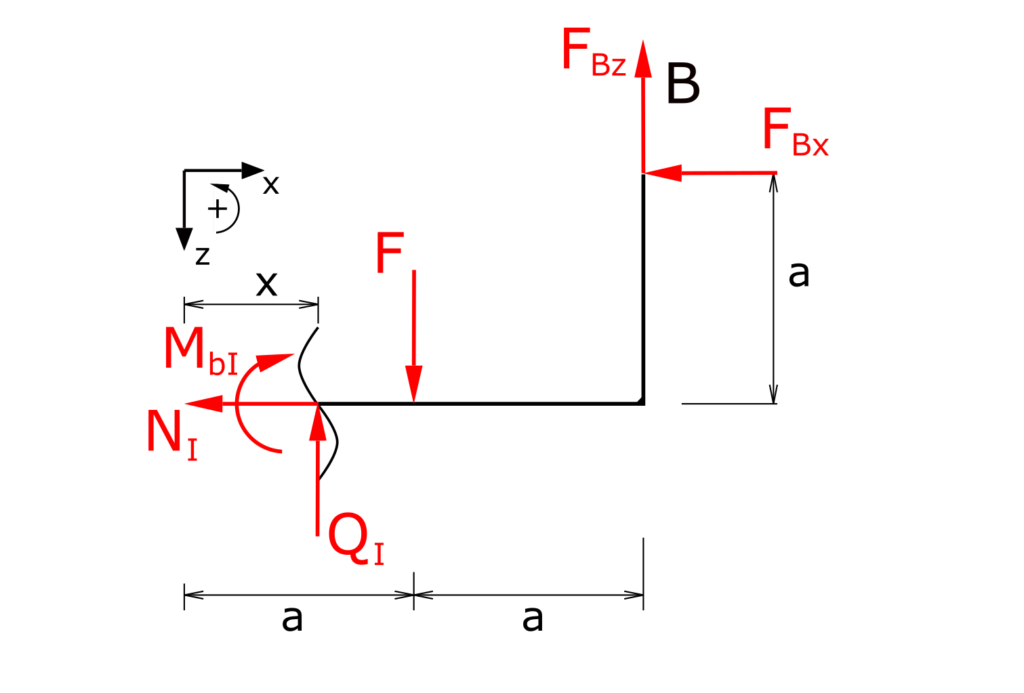
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x-und z-Richtung sowie für die Momente
\[ \tag{7} \sum F_x = 0 = -N_I -F_{Bx}\]
\[ \tag{8} \sum F_z = 0 = -Q_I + F - F_{Bz} \]
\[ \tag{9} \sum M(x) = 0 = -M_{bI} - F \cdot (a-x) + \bcancel{F_{Bx} \cdot a} + F_{Bz} \cdot (2a - x)\]
Mit den bereits berechneten Lagerreaktionen ergeben sich die Schnittgrößen zu
\[ \tag{10} N_I = 0 \]
\[ \tag{11} Q_I = \frac{F}{2} \]
\[ \tag{12} M_{bI} = \frac{F}{2} \cdot x \]
Ermittlung der Schnittgrößen in Bereich II
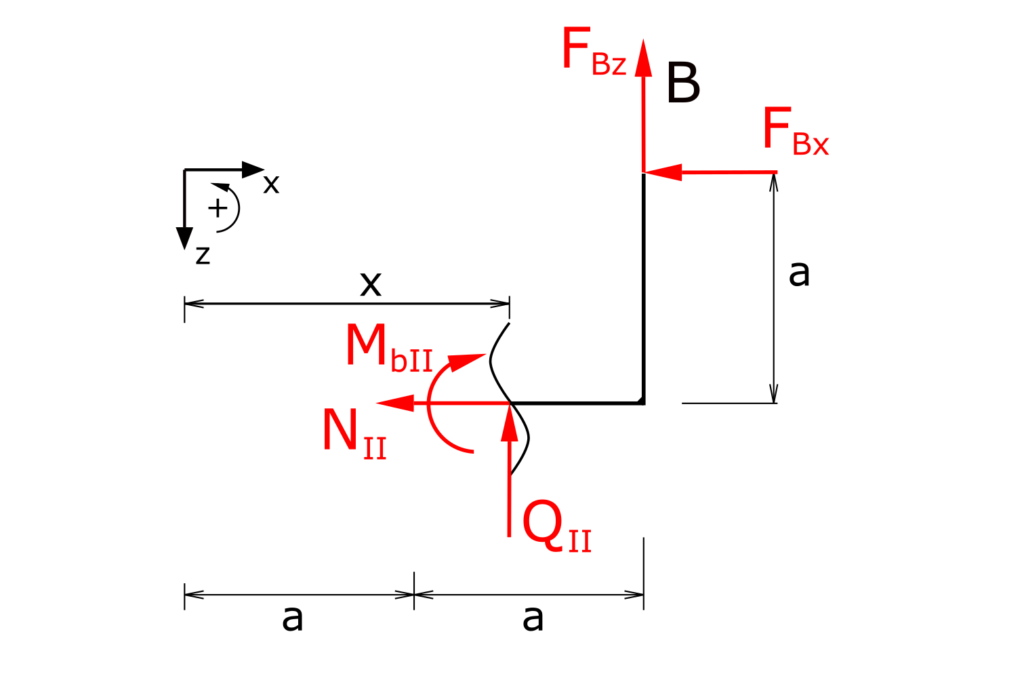
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x-und z-Richtung sowie für die Momente
\[ \tag{13} \sum F_x = 0 = -N_{II} - F_{Bx}\]
\[ \tag{14} \sum F_z = 0 = -Q_{II} - F_{Bz} \]
\[ \tag{15} \sum M(x) = 0 = - M_{bII} + \bcancel{F_{Bx} \cdot a} + F_{Bz} \cdot (2a - x) \]
Auch diese Schnittgrößen lassen sich nach Einsetzen der Lagerreaktionen in B auflösen zu
\[ \tag{16} N_{II} = 0 \]
\[ \tag{17} Q_{II} = - \frac{F}{2} \]
\[ \tag{18} M_{bII} = \frac{F}{2} \cdot (2a - x) \]
Ermittlung der Schnittgrößen in Bereich III
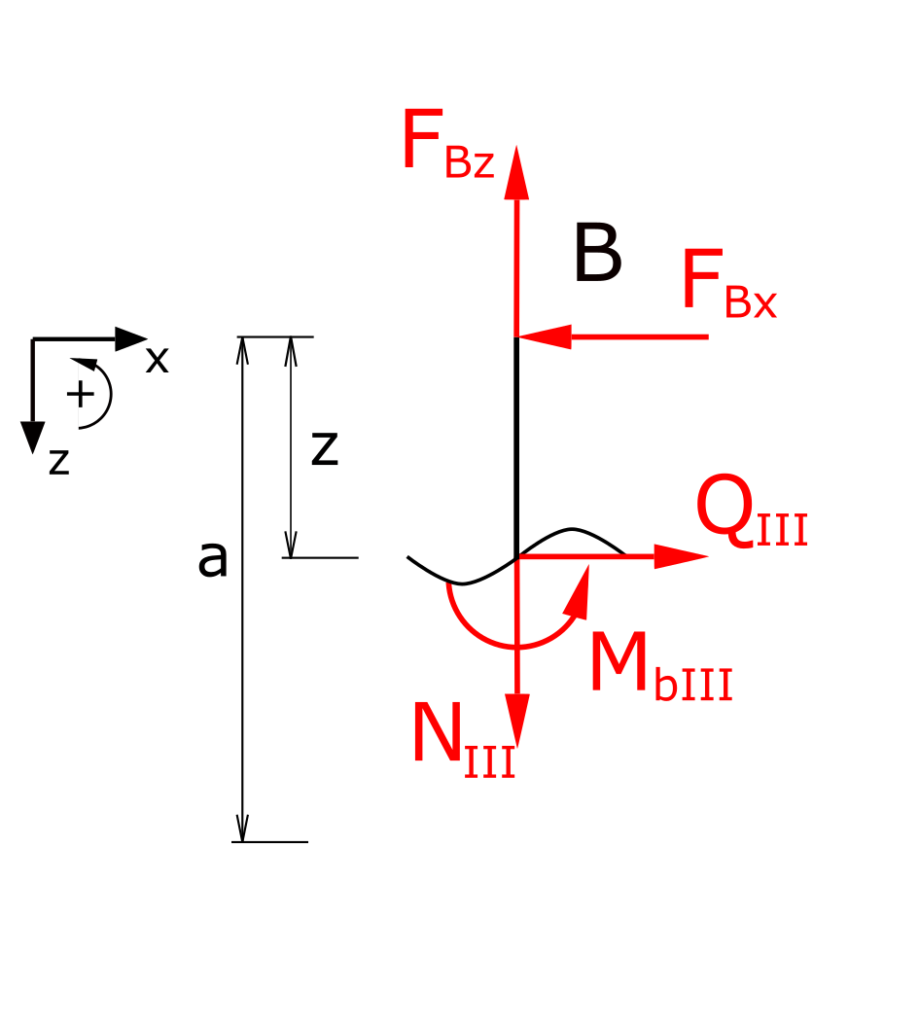
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x-und z-Richtung sowie für die Momente
\[ \tag{19} \sum F_x = 0 = -F_{Bx} + Q_{III}\]
\[ \tag{20} \sum F_z = 0 = N_{III} - F_{Bz} \]
\[ \tag{21} \sum M(z) = 0 = M_{bIII} + \bcancel{F_{Bx} \cdot (z-a)} \]
Die Schnittgrößen des dritten Abschnitts ergeben sich zu
\[ \tag{22} N_{III} = \frac{F}{2} \]
\[ \tag{23} Q_{III} = 0 \]
\[ \tag{24} M_{bIII} = 0 \]
Damit sind alle Schnittgrößen des abgewinkelten Trägers bestimmt.
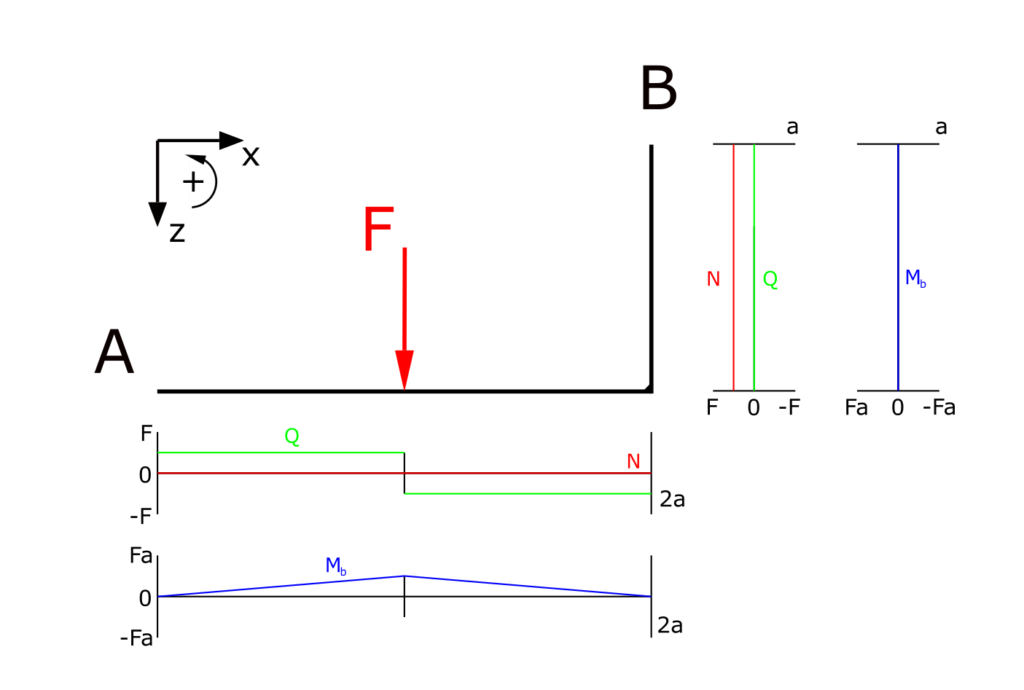
Grafische Darstellung der Schnittgrößen
Die grafische Darstellung der Verläufe der Normalkraft, der Querkraft und des Biegemoments sieht folgendermaßen aus:
Werbung




