Werbung
In dieser Übung werden die Bremsmomente für eine Trommel mit Bremse im Rechtslauf und Linkslauf berechnet.
Reibwerte für verschiedenen Materialpaarungen sind hier zu finden.
Aufgabe
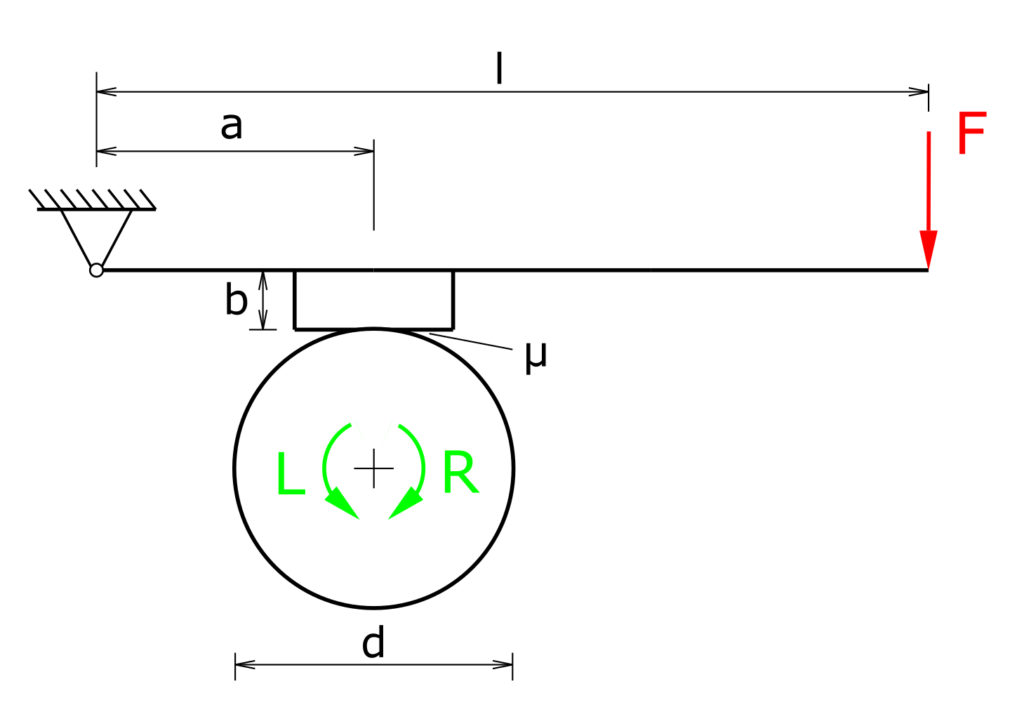
Eine Trommel wird mit einem Bremsklotz, der mit einem Betätigungshebel angedrückt wird, gebremst. Die Trommel kann sowohl im Linkslauf als auch im Rechtslauf betrieben werden.
a) Wie groß sind die Bremsmomente für Links- und Rechtslauf?
b) Wie groß muss die Höhe b sein, damit die Bremsmomente für Rechts- und Linkslauf gleich groß sind?
c) Bei welcher Höhe b tritt ein "Festfressen" der Bremse auf? Passiert dies im Rechts- oder Linkslauf?
Lösung
Die beiden Bremsmomente errechnen sich für den Rechts- und Linkslauf aus der Reibkraft FBx und dem halben Trommeldurchmesser.
\[ M_{BL}=-F_{Bx} \cdot \frac{d}{2} \]
\[ M_{BR}=F_{Bx} \cdot \frac{d}{2} \]
Der Zusammenhang zwischen der Reibkraft und der Normalkraft führt zu
\[ F_{Bx}=µ \cdot F_{By} \]
\[ F_{By} = \frac{F_{Bx}}{µ} \]
Die im folgenden aufgestellten Momentenbilanzen werden bezüglich Punkt A am Betätigungshebel aufgestellt. Linksdrehende Momente sind positiv.
Linkslauf
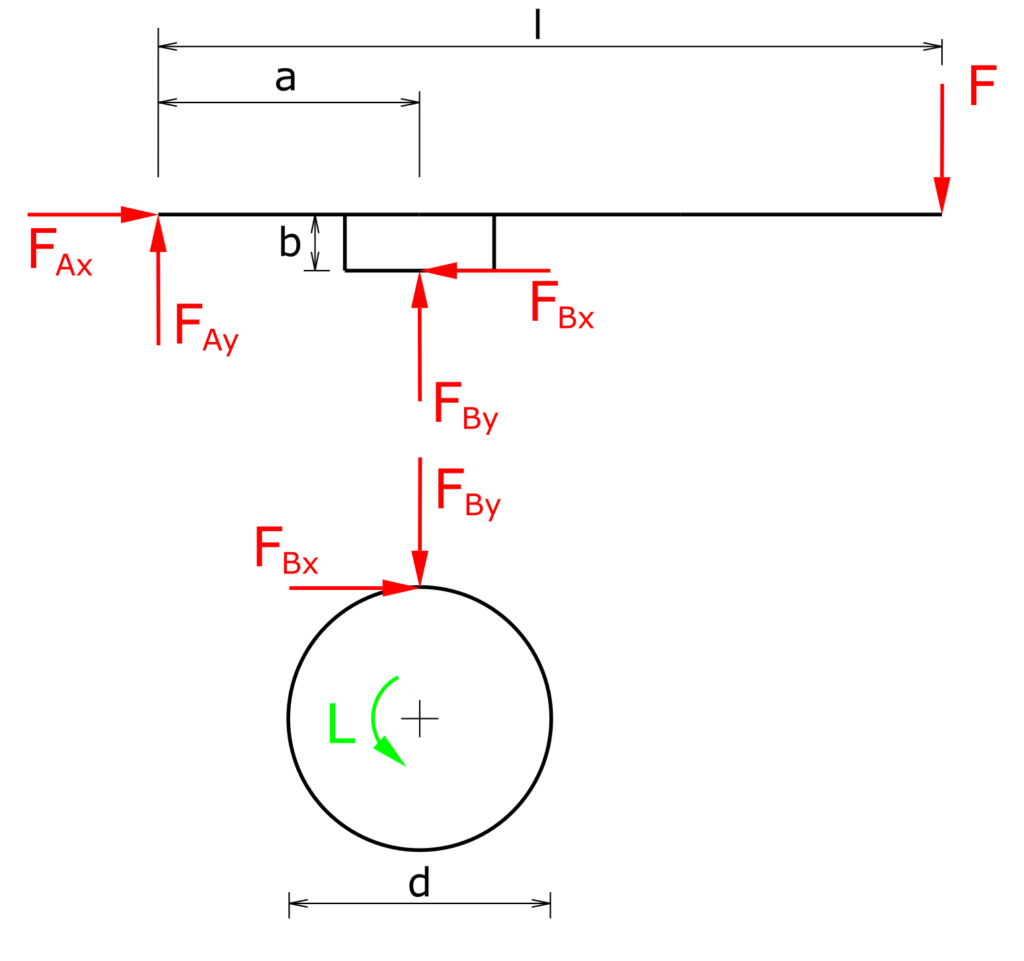
\[ \sum M(A)=0=- F_{Bx} \cdot b + F_{By} \cdot a - F \cdot l \]
\[ 0=-F_{Bx} \cdot b + \frac{F_{Bx}}{µ} \cdot a - F \cdot l \]
\[ F \cdot l=-F_{Bx} \cdot \left( b - \frac{a}{µ} \right) \]
\[ F_{Bx} = - \frac{F \cdot l}{\left( b - \frac{a}{µ} \right)} \]
Das Bremsmoment für den Linkslauf beträgt
\[ M_{BL}=\frac{F \cdot l \cdot d}{2 \cdot \left( b - \frac{a}{µ} \right)} \]
Rechtslauf
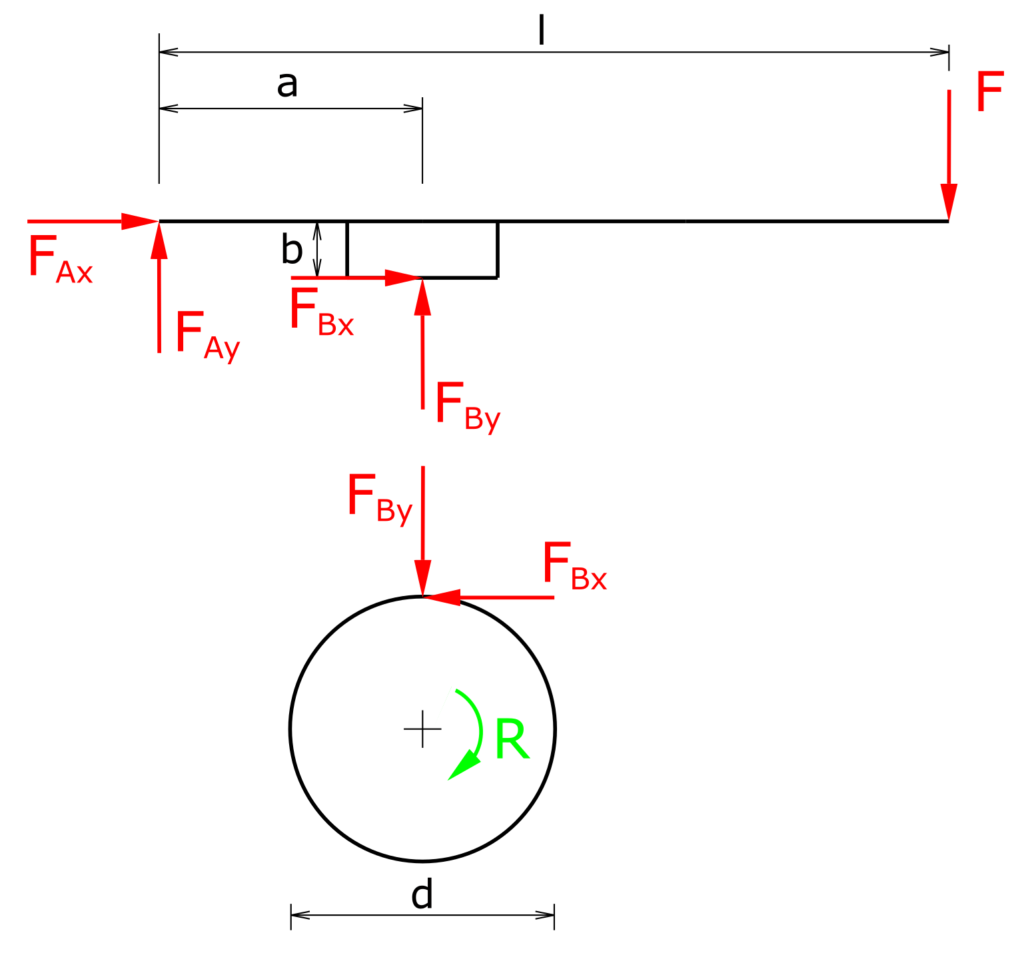
\[ \sum M(A)=0= F_{Bx} \cdot b + F_{By} \cdot a - F \cdot l \]
\[ 0= F_{Bx} \cdot b + \frac{F_{Bx}}{µ} \cdot a - F \cdot l \]
\[ F \cdot l= F_{Bx} \cdot \left( b + \frac{a}{µ} \right) \]
\[ F_{Bx} = \frac{F \cdot l}{\left( b + \frac{a}{µ} \right)} \]
Das Bremsmoment für den Rechtslauf beträgt
\[ M_{BR}= \frac{F \cdot l \cdot d}{2 \cdot \left( b + \frac{a}{µ} \right)} \]
Der Betrag des Bremsmomentes im Linkslauf ist höher als im Rechtslauf, da der Divisor im Rechtslauf größer ist. Die Bremse ist daher im Linkslauf wirksamer als im Rechtslauf.
Ermittlung der Höhe b für ein gleich großes Bremsmoment im Rechts- und Linkslauf
Die Bedingung lautet: MBR = -MBL. Daraus folgt
\[ M_{BR} = M_{BL}\]
\[ \frac{F \cdot l \cdot d}{2 \cdot \left( b + \frac{a}{µ} \right)} = -\frac{F \cdot l \cdot d}{2 \cdot \left( b - \frac{a}{µ} \right)}\]
\[ b + \frac{a}{µ} = - b + \frac{a}{µ} \]
\[ b =0 \]
Ermittlung der Höhe b und Drehrichtung für Festfressen
Die Bremse frisst sich fest, wenn das Bremsmoment gegen unendlich geht. Das kann nur im linksdrehenden Betrieb vorkommen, wenn der Ausdruck unterhalb des Bruchstrichs gegen Null geht.
\[ M_B \rightarrow \infty \]
\[ M_{BL}=\frac{F \cdot l \cdot d}{2 \cdot \left( b - \frac{a}{µ} \right)} \]
\[ b - \frac{a}{µ} = 0 \]
\[ b = \frac{a}{µ} \]
Damit sind alle geforderten Eigenschaften der Trommel mit Bremse im Rechtslauf und Linkslauf bestimmt.
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Reibung.
Werbung




