This exercise addresses the following questions:
- What moment arises when a force is shifted parallel to its effective direction?
- How can you calculate the moment for a force acting at an angle?
- How do you calculate the lever arm of an attacking force?
Task
The force F shall be shifted into point P. Which moment results?
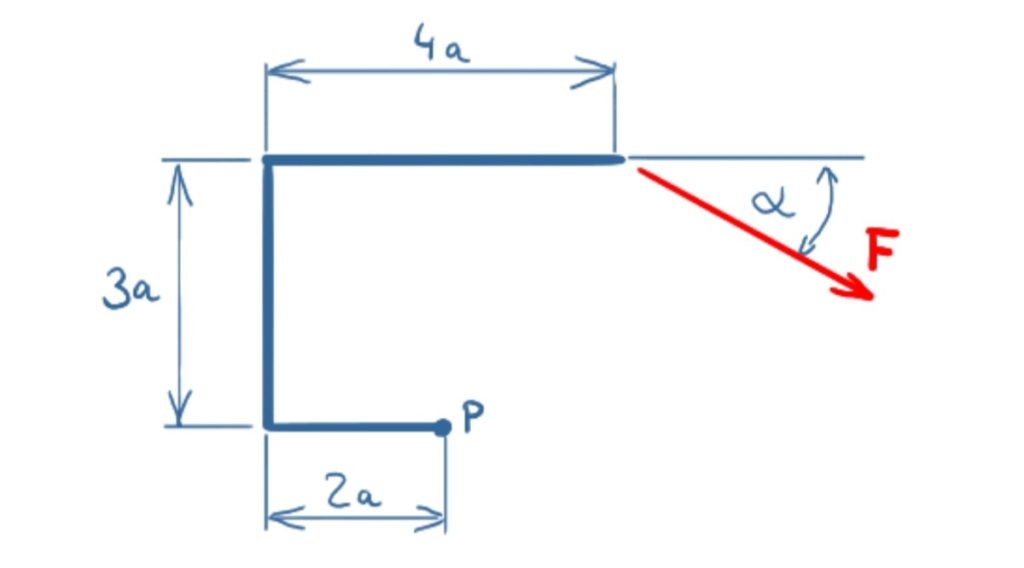
Solution
The following video is in german language and describes the first (more complicated) way of solution.
Shifting a force parallel to its effective direction creates a moment, also known as an offset moment. The lever arm of the moment is the amount of displacement.
Solution approach 1
In approach 1, calculations are carried out without the decomposition of forces. It is more complex than the second approach.
Geometrical conditions for the calculation
The way in which the sketch for the task is carried out suggests that the lever arm for the force F can be calculated directly using the Pythagorean theorem and the edge lengths 3a and 4a-2a = 2a. But this is a fallacy, because as soon as you make the sketch for a changed angle, you can see that the lever arm must be determined as in the following sketch.
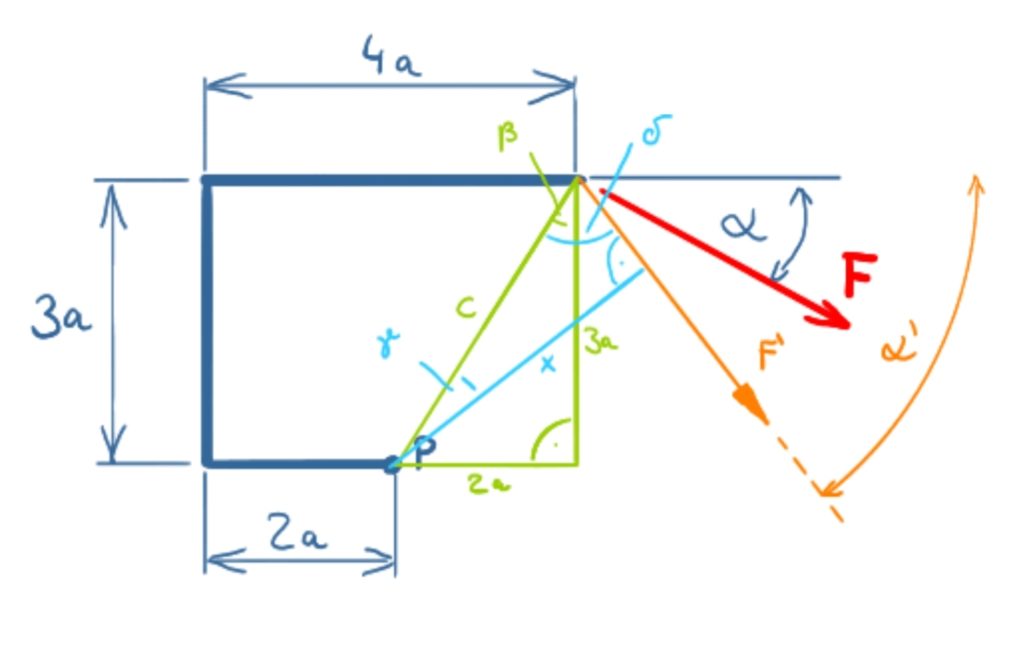
The math
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]Since the solution has to be found for an arbitrary angle α, the forces F' and α' have been added in the solution sketch to clarify the geometrical relationships. In the following formulas, however, the values F and α are used. In the solution described here, right-turning moments were defined as positive (in the solution video, left-turning moments were assumed to be positive). The moment in point P is calculated from
\[\tag{1} M_P = F \cdot x \]
The lever arm x is made up
\[\tag{2} x = c \cdot \cos \gamma \]
Side c can be calculated using the Pythagorean Theorem.
\[\tag{3} c = \sqrt{3^2a^2+2^2a^2} \]
\[\tag{4} c = \sqrt{13}a \]
The angles are related as follows:
\[\tag{5} \gamma = 90° - \delta \]
\[\tag{6} \delta = 90° - \alpha + \beta \]
\[\tag{7} \beta = arctan \left( \frac{2\bcancel{a}}{3\bcancel{a}} \right) = 33.7° \]
\[\tag{8} \delta = 123.7° - \alpha \]
\[\tag{9} \gamma = \alpha - 33.7° \]
The lever arm x can now be determined
\[\tag{10} x = \sqrt{13}a \cdot \cos (\alpha - 33.7°) \]
And finally the resulting moment
\[\tag{11} M_P = F \cdot \sqrt{13}a \cdot \cos (\alpha - 33.7°) \]
The resulting moment can also be determined by decomposition of the force into its components:
Solution approach 2
This solution is based on an x-y coordinate system and the forces are broken down into their components. Right turning moments are positive again. The two components of the acting force F are:
\[\tag{1} F_x = F \cdot cos \alpha \]
\[\tag{2} F_y = F \cdot sin \alpha \]
The resulting moment follows from:
\[\tag{3} M_P = F \cdot cos \alpha \cdot 3a + F \cdot sin \alpha \cdot 2a \]
\[\tag{4} M_P = F \cdot a \cdot (3 \cdot cos \alpha + 2 \cdot sin \alpha) \]
The second way to solve this problem is much easier than the first one.
Here we have some more exercises about the determination of resulting moments.

