Task
A belt drives a roller with a force A = 890 N in the load side and a wrap angle α = 160 °. The coefficient of static friction is µ0 = 0.3.
a) How big is the force L in the loose belt?
b) How big must the wrap angle α' be if the force in the work belt is increased to A' = 1,100 N while the force L in the loose belt remains the same?
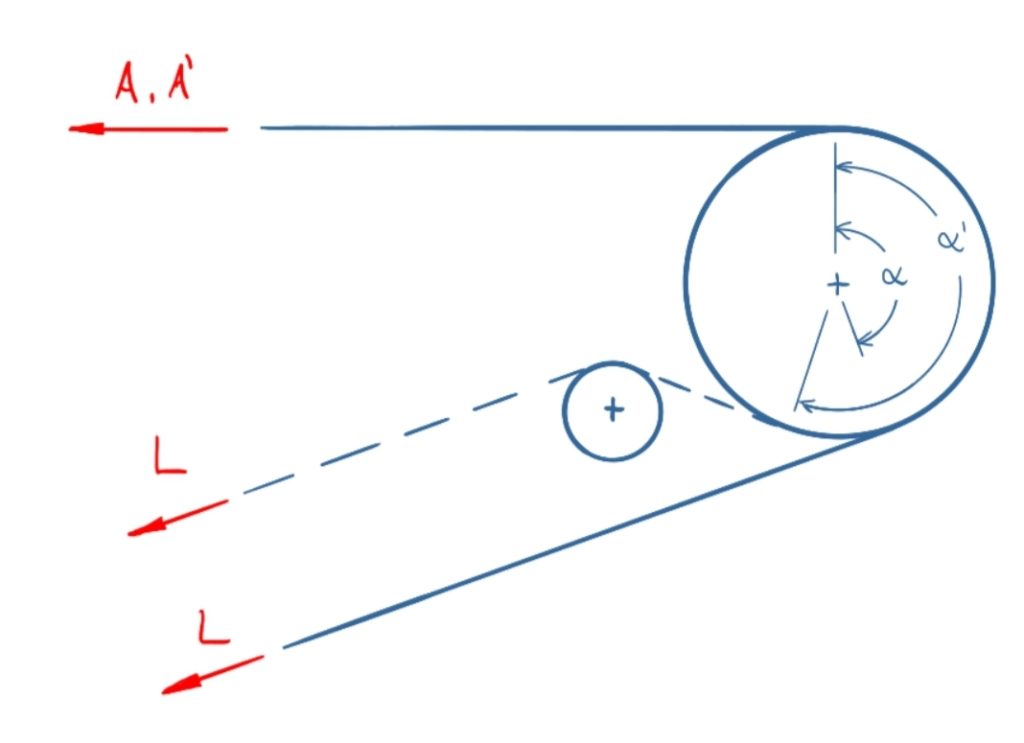
Solution
The relationship between the forces in the work belt and in the loose belt is described by the belt friction formula (Euler-Eytelwein).
\[ \require{cancel} \]reg. a), value of the force L
\[ \tag{1} A \leq L \cdot e^{µ_0 \cdot \alpha} \]
The inequalition is simplified in the following to
\[ \tag{2} L = A \cdot e^{-µ_0 \cdot \alpha} \]
\[ \tag{3} L = 890 N \cdot e^{-0.3 \cdot \frac{8}{9} \cdot \pi} \]
\[ \tag{4} L = 385 N \]
reg. b), increased force in the work belt
The calculation of the required wrap angle for the increased tensile force in the load side is carried out using the following relationship
\[ \tag{5} L = A' \cdot e^{-µ_0 \cdot \alpha\,'} \]
\[ \tag{6} \frac{A'}{L} = e^{µ_0 \cdot \alpha\,'} \]
\[ \tag{7} \alpha\,' = \frac{\ln \left( \frac{A'}{L} \right)}{µ_0} \]
\[ \tag{8} \alpha\,' = \frac{\ln \left( \frac{1100 N}{385 N} \right)}{0.3} \]
The necessary wrap angle is therefore in radians
\[ \tag{9} \alpha\,' = 3,5 rad \]
or converted into °
\[ \tag{10} \alpha\,' = 200° \]

