Task
The common center of area has to be calculated for the shown circular cross-section with a bore.
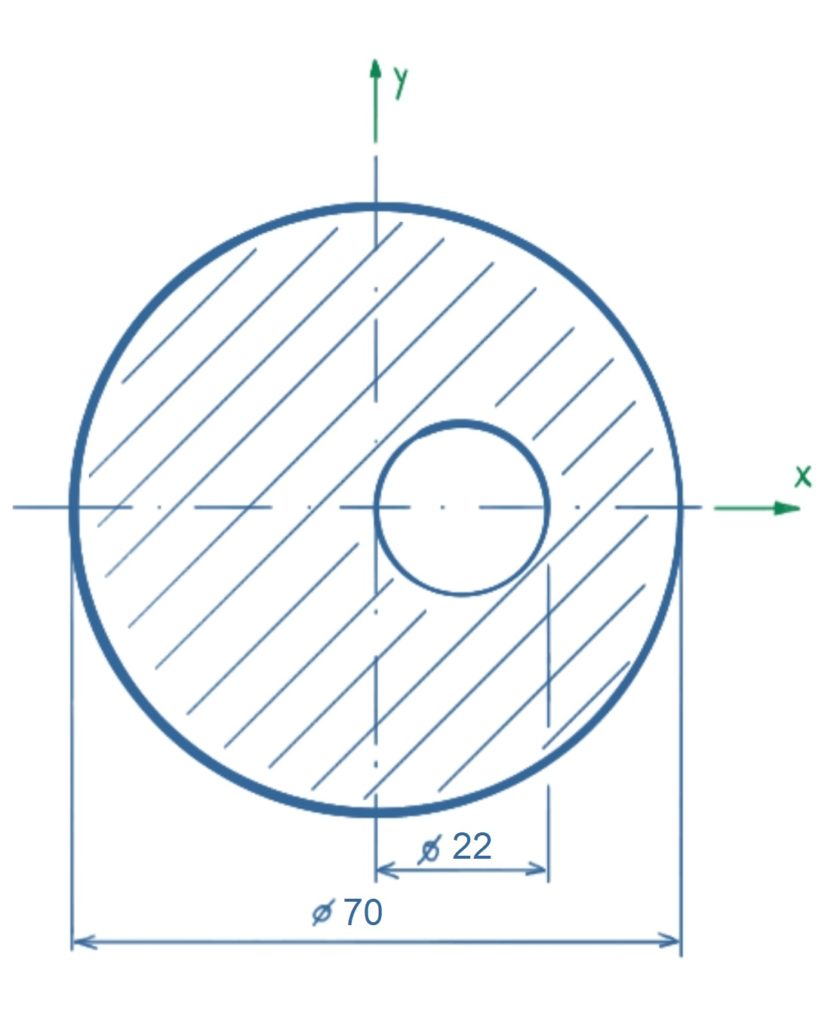
Solution
The individual areas are numbered in the first step.
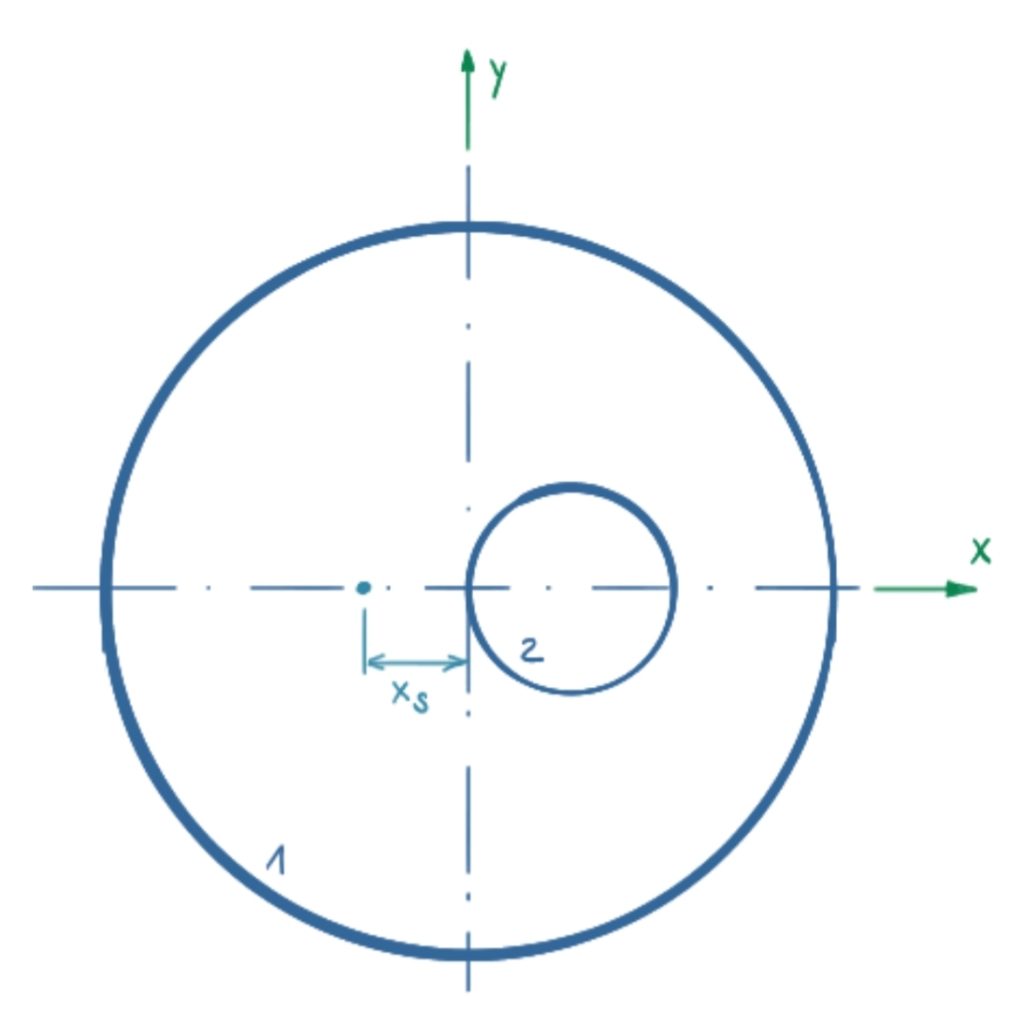
Since the component is mirror-symmetrical about the x-axis, it is sufficient to consider the x-coordinate. The general equation for the x-coordinate of the center of area is:
\[ \tag{1} x_S = \frac{\sum A_i \cdot x_i}{\sum A_i} \]
And for the area of the circle
\[ \tag{2} A = \frac{\pi}{4} \cdot d^2 \]
The individual areas and their centre point coordinates are listed in a table. Empty areas, such as e.g. the bore with the diameter of 22mm, are negative.
| \[ i \] | \[ A_i \] | \[ x_i \, in \, mm \] | \[ A_i \cdot x_i\, in \,mm^3 \] |
|---|---|---|---|
| 1 | 3.848 | 0 | 0 |
| 2 | -380 | 11 | -4.180 |
| \[ \sum \] | 3.468 | -4.180 |
\[ \tag{3} x_S = \frac{-4180mm^3}{3468mm^2} \]
\[ \tag{4} x_S = -1,21 mm \]
And for the sake of completeness:
\[ \tag{5} y_S = 0 mm \]

