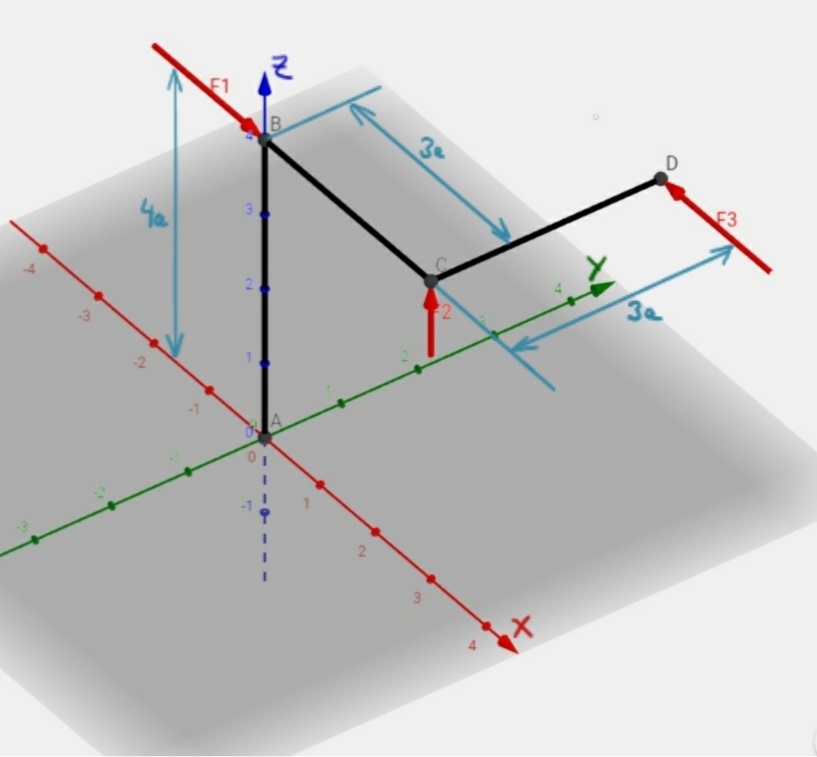
Task
The forces F1, F2 and F3 act on a frame as shown. The acting forces have to be summarized in point A and point B. Calculate the resultant force and the resulting moments.
given: F1 = 2F, F2 = F, F3 = 2F, a
Solution
The following video is in german language.
The force vectors are
The position vectors have to be defined separately for the two cases to be considered. For the resulting moment at point A they are
For the resulting moment in point B they are
The resulting force is the same regardless of whether it is calculated for A or B:
\[\tag{4} \sum \vec{F_A} = \sum \vec{F_B} = \vec{F_1} + \vec{F_2} + \vec{F_3} \]
\[\tag{5} \sum \vec{F} = \myvec{2F\\0\\0} + \myvec{0\\0\\F} + \myvec{-2F\\0\\0} \]
\[\tag{6} \sum \vec{F} = \myvec{0\\0\\F} \]
The resulting moment at point A results from the sum of the cross products of the force and position vector, based on A. The procedure for calculating the cross product is described in the video above. The Sarrus rule is applied there.
\[\tag{7} \sum \vec{M_A} = \vec{r_{1A}} \times \vec{F_1} + \vec{r_{2A}} \times \vec{F_2} + \vec{r_{3A}} \times \vec{F_3} \]
\[\tag{8} \sum \vec{M_A} = \myvec{0\\0\\4a} \times \myvec{2F\\0\\0} + \myvec{3a\\0\\4a} \times \myvec{0\\0\\F} + \myvec{3a\\3a\\4a} \times \myvec{-2F\\0\\0} \]
\[\tag{9} \sum \vec{M_A} = \myvec{0\\-3Fa\\6Fa} \]
For the resulting moment at point B, the equation is
\[\tag{10} \sum \vec{M_B} = \vec{r_{1B}} \times \vec{F_1} + \vec{r_{2B}} \times \vec{F_2} + \vec{r_{3B}} \times \vec{F_3} \]
\[\tag{11} \sum \vec{M_B} = \myvec{0\\0\\0} \times \myvec{2F\\0\\0} + \myvec{3a\\0\\0} \times \myvec{0\\0\\F} + \myvec{3a\\3a\\0} \times \myvec{-2F\\0\\0} \]
\[\tag{12} \sum \vec{M_B} = \myvec{0\\-3Fa\\6Fa} \]
The fact that these two moments are equal in this case is due to the geometric arrangement in this exercise, i.e. it is more likely that the consideration of different points also leads to different moment vectors.

