Task
A railway wagon stands on a sloping track on a (frictionless) buffer stop. Which reaction forces occur on the wheels and on the buffer stop?
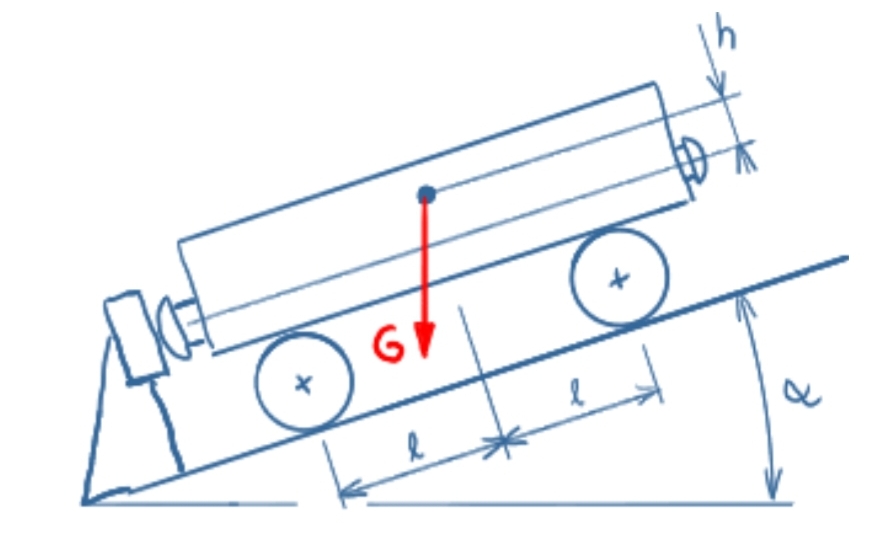
Solution
The following video is in german language.
Solution sketch
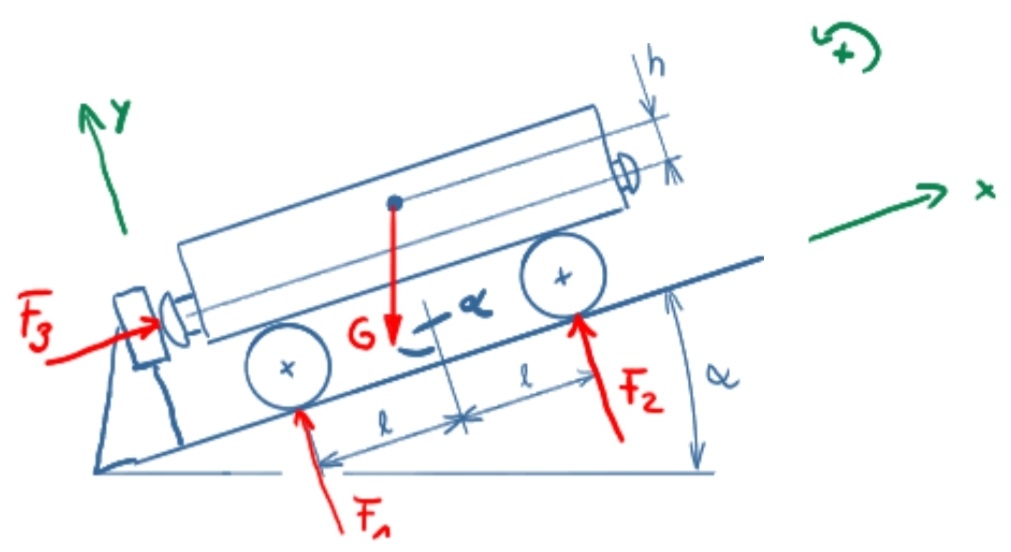
Solution approach
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]The coordinate system is rotated by the angle α to solve the problem. Left turning moments are positive.
The equilibrium of forces in the x-direction is
\[\tag{1} \sum F_x = 0 = F_3 - G \cdot \sin \alpha \]
\[\tag{2} F_3 = G \cdot \sin \alpha \]
The equilibrium of forces in the y-direction is
\[\tag{3} \sum F_y = 0 = F_1 - G \cdot \cos \alpha + F_2 \]
Due to the geometric specifications, the equilibrium of moments can only be considered around G and leads to
\[\tag{4} \sum M(G) = 0 = F_3 \cdot h - F_1 \cdot l + F_2 \cdot l \]
\[\tag{5} 0 = G \cdot \sin \alpha \cdot h - F_1 \cdot l + F_2 \cdot l \]
\[\tag{6} F_2 = \frac{F_1 \cdot l - G \cdot \sin \alpha \cdot h}{l} \]
From equation 3 follows
\[\tag{7} 0 = F_1 - G \cdot \cos \alpha + \frac{F_1 \cdot l - G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{8} G \cdot \cos \alpha = F_1 + \frac{F_1 \ \cdot \bcancel{l}}{\bcancel{l}} - \frac{G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{9} F_1 = \frac{G}{2} \cdot \left( \cos \alpha + \frac{\sin \alpha \cdot h}{l} \right) \]
F2 follows from equation 6
\[\tag{10} F_2 = \frac{\frac{G}{2} \cdot \left( \cos \alpha + \frac{\sin \alpha \cdot h}{l} \right) \cdot l - G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{11} F_2 = \frac{ \frac{G}{2} \cdot \cos \alpha \cdot l + \frac{G}{2} \cdot \frac{\sin \alpha \cdot h}{\bcancel{l}} \cdot \bcancel{l} - G \cdot \sin \alpha \cdot h}{l} \]
\[\tag{12} F_2 = \frac{ G \cdot \cos \alpha \cdot l - G \cdot \sin \alpha \cdot h}{2 \cdot l} \]

